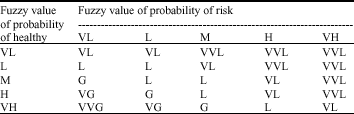
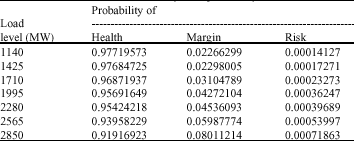
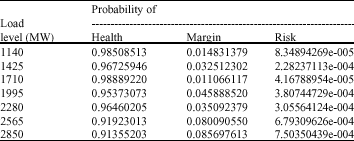
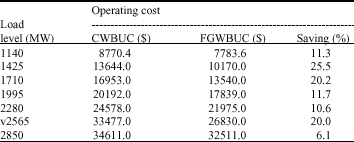
Research Article
Introduction of a Hybrid Method for Determination of Operating Reserve in the Well-Being Framework
Department of Electrical Engineering, Imam Khomeini International University, Qazvin, Iran
N. Bigdeli
Department of Electrical Engineering, Imam Khomeini International University, Qazvin, Iran