ABSTRACT
The primary objective of this study is to solve the Vehicle Routing Problem with Stochastic Demands (VRPSD) under restocking policy by using adaptive Genetic Algorithm (GA). The problem of VRPSD is one of the most important and studied combinatorial optimization problems, which finds its application on wide ranges of logistics and transportation area. It is a variant of a Vehicle Routing Problem (VRP). The algorithms for stochastic VRP are considerably more intricate than deterministic VRP and very time consuming. This has led us to explore the used of metaheuristics focusing on the permutation-based GA. The GA is enhanced by automatically adapting the mutation probability to capture dynamic changing in population. The GA becomes a more effective optimizer where the adaptive schemes are depend on population diversity measure. The proposed algorithm is compared with standard GA on a set of randomly generated problems following some discrete probability distributions inspired by real case of VRPSD in solid waste collection in Malaysia. The performances of several types of adaptive mutation probability were also investigated. Experimental results show performance enhancements when adaptive GA is used.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.3228.3234
URL: https://scialert.net/abstract/?doi=jas.2008.3228.3234
INTRODUCTION
Vehicle Routing Problem (VRP) is often faced by distribution and logistic-transportation companies. Usually many companies use classical deterministic VRP models on their routing that do not capture an important aspect of real life problems. In real life problems, the parameters (demand, time, city location, etc.) are often stochastic or random. It is appropriate to model the stochasticity of real world situation by using VRP with Stochastic Demands (VRPSD) model to produce better routes and reduce cost. In VRPSD, the customer demands are unknown until the vehicle arrives at customer locations but it is assumed to follow a specific probability distribution according to the past customer demands behaviour. One of the applications is in the case of a solid waste collection problem where it is impossible to know the exact amount of garbage to be collected at the time when the route is planned.
In stochastic environment, due to its randomness in customers` demands, a vehicle capacity may be exceeded during service. A route failure is said to occur if the demand exceeds capacity and a recourse action needs to be taken. Assuming that enough capacity is available at the depot, the vehicle may return to the depot, replenish its load and then resume service at the point where failure occurred. Therefore the vehicle will always be able to satisfy all demands and the length of the corresponding tour becomes a random quantity. In the literature, VRPSD has been studied under two distinct approaches. The recourse action could be the vehicle resumes service along the planned route, namely a priori approach, or visiting the remaining customers possibly in an order that differs from the planned sequence that is called re-optimization approach. There are two common recourse policies for a priori optimization. The first is the simple recourse policy (Gendreau et al., 1995; Chepuri and Homem-de-Mello, 2005), a vehicle returns to the depot to restock when its capacity becomes attained or exceeded. In the second approach (Bertsimas et al., 1995; Yang et al., 2000; Bianchi et al., 2004), preventive restocking is planned at strategic points preferably when the vehicle is near to the depot and its capacity is almost empty, along the scheduled route instead of waiting for route failure to occur. On the other hand, two most recent computational studies in re-optimization approach are done by Secomandi (2001, 2003).
Stochastic VRPs are considerably more intricate and very time consuming than the deterministic one. It requires the development of new ideas and algorithm that can solve problem in realistic time and reasonable solution quality. The class of VRPs being addressed is a difficult one, since its elements are usually NP-hard problems. They are generally solved by heuristic methods (Secomandi, 2003). Beside the work of Bianchi et al. (2004), the work on the application of GA in VRPSD is very lacking in the literature, although as known for many years, GA has been successfully used in a wide variety of problem domains including VRP. In majority of GA implementation, the operator settings are remaining static during the GA run. However, some existing works found were showed that varying GA settings during the GA application can lead to improvement of GA performance. Herrera and Lozano (1996) have reviewed many aspects of the adaptation of GA parameters settings such as mutation probability (pm), crossover probability (pc) and population size (N).
The awareness of the importance of mutation is growing within the evolutionary algorithm community and interest is increasing in a closer consideration of its features (De Falco et al., 2002). Mutation operator may be considered to be an important element in GA for solving the premature convergence problem, since, it serves to create random diversity in the population. If the lack of population diversity takes place too early, a premature stagnation of the search is caused. Under these circumstances, the search is likely to be trapped in a local optimum before the global optimum is found. Most approaches adapt pm along with other GA parameters (Lee and Takagi, 1993; Srinivas and Patnaik, 1994; Sugisaka and Fan, 2001; Mei-Yi et al., 2004; Xing et al., 2007) and so, the specific effects of the adaptation of pm alone were not studied. Lee and Takagi (1993) presented experimental study which was aimed at isolating the effects of the adaptation by Fuzzy Logic Controllers of N, pc and pm. It showed that the adaptation of pm contributes most to high performance.
A time-dependency of pm was first suggested by Holland (1992) although he did not give a detailed choice of the parameter for the time-dependent reduction of pm. The idea of sustaining genetic diversity through mutation is then developed by measuring the Hamming distance between the two parents during reproduction. One of it was done by Herrera and Lozano (1996) using the adaptive control of pm by Fuzzy Logic Controllers. Reeves (1995) used adaptive mutation rate allowing high mutation rate and slowly decreased as long as a reasonably diverse population exists. Liu and Feng (2004) presented a modified GA based on tuning of pm by the value of individual fitness. The modified GA implements mutation first, after that crossover.
This study contributes mainly on presenting an adaptive GA based on diversity measures for a priori VRPSD. We also proposed a new adaptive mutation probability based on Lr distance measure. The performance of several adaptive mutation probability types on VRPSD was also studied for the first time. In this study, the VRPSD recourse action is under restocking policy.
VEHICLE ROUTING PROBLEM WITH STOCHASTIC DEMANDS
The VRPSD is defined on a complete graph:
G = (V, A, C) |
| V | = | {0, 1,. .., n} is a set of nodes with node 0 denotes the depot and nodes 1, 2, ..., n correspond to the customers, |
| A | = | {(i, j) : i, j ∈ V, i ≠ j} is the set of arcs joining the nodes,and a non-negative matrix |
| C | = | {cij : i, j ∈ V, i ≠ j} denotes the travel costs (distances) between node i and j. |
The cost matrix C is symmetric and satisfies the triangular inequality. Customers have stochastic demands ξi, i = 1,..., n which follows known probability distributions pik = pr ob(ξi = k), k = 0, 1, 2, ..., K. Assume further that customers` demands are independent. Actual demand of each customer is only known when the vehicle arrives at the customer location. A feasible solution to the VRPSD is a permutation of the customers s = (s(1), s(2),. .., s(n)) starting at the depot (that is, s(1) = 0) and it is called a priori tour. Let 0 →1 →2 ... j →j+1 ... →n be a particular vehicle route. Upon the service completion at customer j, suppose the vehicle has a remaining load q (or the residual capacity of the vehicle after having serviced customer j) and let fj(q) denote the total expected cost from node j onward. If Sj represents the set of all possible loads that a vehicle can have after service completion at customer j, then, fj(q) for q ∈ Sj satisfies:
(1) |
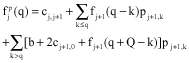 | (2) |
(3) |
with the boundary condition:
(4) |
In Eq. 2-4,![]() represents the expected cost of going directly to the next node, whereas
represents the expected cost of going directly to the next node, whereas ![]() represents the expected cost of the restocking action. Equation 2-4 are used to recursively determine the objective value of the planned vehicle route and the optimal sequence of decisions after customers are served (Bianchi et al., 2004). In principle, this procedure leads to a dynamic programming since each time a customer demand is revealed, a decision has to be taken as to where the vehicle should proceed.
represents the expected cost of the restocking action. Equation 2-4 are used to recursively determine the objective value of the planned vehicle route and the optimal sequence of decisions after customers are served (Bianchi et al., 2004). In principle, this procedure leads to a dynamic programming since each time a customer demand is revealed, a decision has to be taken as to where the vehicle should proceed.
The expected cost-to-go in case of restocking, is constant in q, since in case of restocking the vehicle will have full capacity Q before serving the next customer, whatever the current capacity q is. On the other hand, ![]() is a monotonically non-increasing function in q, for every fixed customer j. Therefore there is a capacity threshold value hj such that, if the vehicle has more than this value of residual goods, then the best policy is to proceed to the next planned customer, otherwise it is better to go back to the depot for replenish (Yang et al., 2000).
is a monotonically non-increasing function in q, for every fixed customer j. Therefore there is a capacity threshold value hj such that, if the vehicle has more than this value of residual goods, then the best policy is to proceed to the next planned customer, otherwise it is better to go back to the depot for replenish (Yang et al., 2000).
DATA
VRPSD application is considered in the solid waste collection problem of residential area in Malaysia. The problem of optimization of waste collection can be described as follows. The solid waste is located in box or containers along the streets and they must be all collected by a fleet of vehicles whose capacity can not be exceeded. Each vehicle can service several such sites before going to dumpsite to unload. Each vehicle starts from the depot, visits a number of stops and ends at the depot. When a vehicle is full, it needs to go to the closest available dumpsite to empty its load and then resume their visit. Each vehicle can make multiple disposal trips per day.
Based on experiments reported in Gendreau et al. (1995), three factors seem to impact the difficulty of a given VRP instances: number of customers` n, number of vehicles m and filling coefficient f. In a stochastic environment, the filling coefficient can be defined as:
(5) |
where, E(ξi) is the expected demand of customer i and Q denotes the vehicle capacity. This is the measure of the total amount of expected demand relative to vehicle capacity and can be approximately interpreted as the expected number of loads per vehicle needed to serve all customers. In this experiment, the value of f is 1.1.
A set of data are randomly generated to simulate this problem of waste collection. n nodes are generated in the [0,100]2 square according to a continuous uniform distribution. Nodes are first assigned to a specific three demand range in equal probabilities. Three ranges of demand present low, medium and high solid waste weight. The value of each demand is then generated in the appropriate range according to a discrete uniform distribution. The sample size of number of nodes and associates demand ranges are described:
| • | Small sample size: n = 10 and n = 15, Demand range: (1, 3), (2, 4), (3, 5) |
| • | Larger sample size: n = 20, n = 30 and n = 50, Demand range: (1, 5), (6, 10), (11, 15) |
THE PROPOSED GENETIC ALGORITHM
The important details of the Genetic Algorithm are outline below.
| Step 0: | (Define): Define operator settings of GA suitable with the problem which is VRPSD. |
| Step 1: | (Initialize): Create an initial population P of N chromosomes that consists of constructive heuristics solutions and randomly mutation of it where all individuals are distinct or clones are forbidden. |
| Step 2: | (Fitness): Evaluate the fitness f(Ci) of each chromosome Ci in the population. The fitness is the function of VRPSD objective function. |
| Step 3: | (Selection): Apply Roulette Wheel Selection. This gives the set of Mating Population M with size N. |
| Step 4: | (Crossover): Pair all the chromosomes in M at random forming N/2 pairs. Apply crossover with probability pc to each pair and form N chromosomes of offspring, if random number ≥ pc then offspring is the exact copy of parents. |
| Step 5: | (Mutation): With a mutation probability pm mutate the offspring. |
| Step 6: | (Replace): Evaluate fitness of parents and new offspring. Choose the best N chromosomes. Replace the old population with newly generated population. |
| Step 7: | (Test): If the stopping criterion is met then stop and return to the best solution in current population, else go to step 2. |
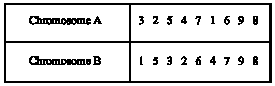 | |
| Fig. 1: | Illustration of order representation |
Chromosome representation: In developing the algorithm, the permutation representation or the path representation or order representation is used since the typical approach using binary strings will simply make coding more difficult. Order representation is perhaps the most natural and useful representation of a VRP tour, where customers are listed in the order in which they are visited. A chromosome represents a route and a gene represents a customer and the values of genes are called alleles. The search space for this representation is the set of permutations of the customers; every chromosome is a string of numbers that represent a position in a sequence. Order representation can be described as shown in Fig. 1.
Initialization: Usually, the initial population of candidate solutions is generated randomly across the search space. However, other information can be easily incorporated to yield better results. The inclusion of good heuristic in initial solution is stated as Prins (2004) by using Clarke and Wright, Mole and Jameson and Gillett and Miller heuristics for solving distance-constrained VRP (DVRP) instances. In this study, Nearest Neighbour (NN) and Farthest Insertion (FI) is included to the initial solution and the rest are the mutation results of NN and FI. The population is an array P of N (population size) chromosomes. Each chromosome Pk is initialized as a permutation of customers. Clones (identical solutions) are forbidden in P to ensure a better dispersal of solutions and to diminish the risk of premature convergence.
The population size is one of the important factors affecting the performance of genetic algorithm. Small population size might lead to premature convergence. On the other hand, large population size leads to unnecessary expenditure of valuable computational time. Prins (2004) stated that population size < 25 or > 50 will give moderate degradation of the average solution and found that population size equal to 30 performs best.
Evaluation: Once the population is initialized or an offspring population is created, the fitness values of candidate solutions are evaluated. The fitness value is the function of VRPSD objective function. The lower the VRPSD objective function means the higher the fitness of solution.
Roulette Wheel Selection with elitism: This research employs the combination of two types of GA selection techniques, namely roulette wheel and elitism. The roulette wheel selection works by selecting the chromosome by looking at their proportional fitness rank. This is where the evolution concept survival of the fittest comes into plays. Some researchers found that this technique will lead to only the best chromosome been selected in the population. It because the fittest chromosome rank is bigger compared to the less fit chromosome and in probability of course chromosome with the highest rate will have a big chance to be selected, while the elitism technique is a simple selection operator, which reserved the best found chromosome in the current population to rebirth for the next generation.
Mitchell (1996) said that elitism could increase rapidly the performance of genetic algorithm, because it prevents losing the best-found solution. When creating a new generation using the reproduction operator, we could have a chance of losing the best-found chromosome in the current population. This is where elitism plays their role in preventing the lost of this chromosome. In this example, after the calculation for each selection chromosome probability has been done, the elitism operator will automatically reserved the chromosome that produce the lowest expected cost.
Order Crossover (OX): Oliver et al. (1987) applied Partially Match Crossover (PMX), Cycle Crossover (CX) and Order Crossover (OX) to the 30-city problem of Hopfield and Tank. They found that the best tour generated with OX was 11% shorter than the best PMX tour and 15% shorter than the best CX tour. In a later study by Starkweather et al. (1991), six different crossover operators were tested on the problem of Hopfield and Tank. Thirty different runs were performed with each operator. In this experiment, OX found the optimum 25 times (out of 30), while PMX found the optimum only once and CX never found the optimum.
Thus in this study, OX was employed in the generation of offspring. OX was first proposed by Oliver et al. (1987). This crossover operator extends the modified crossover of Davis (1991) by allowing two cut points to be randomly chosen on the parent chromosomes. In order to create an offspring, the string between the two cut points in the first parent is first copied to the offspring. Then, the remaining positions are filled by considering the sequence of cities in the second parent, starting after the second cut point (when the end of the chromosome is reached, the sequence continues at position 1). The pc is set to be 0.6 as used by Jerald et al. (2006).
Mutation: Mutation alters one or more genes (positions) of a selected chromosome (solution) to reintroduce lost genetic material and introduce some extra variability into the population. The role of mutation in GAs has been that of restoring lost or unexplored genetic material into the population to prevent premature convergence of the GA sub optimal solutions (Laoufi, 2006; Zuhaimy and Irhamah, 2007). As opposed to the classical mutation operator, which introduces small perturbations into the chromosome, the permutation operators for the VRP and or TSP often greatly modify the original tour. In this study, we implement swap mutation.
The choice of probability of mutation is known to critically affect the behaviour and performance of the GA. Increasing the value of pc and pm promote exploration at the expense of exploitation. The moderately large values of pc promote the extensive recombination of schemata, while small values of pm are necessary to prevent the disruption of the solutions. Several schemes of mutation probability is used including fixed mutation probability and adaptive ones. In fixed mutation probability, the mutation probability remains the same from generation to the next generation. Small values of pm (0.001 until 0.05) that commonly employed in GA practice were implemented (Davis, 1991).
Stopping criterion: In using the optimization algorithms, the goal is to search for the global optimum and it should be found. However, in general it is not clear when the goal is achieved especially in our application in the real world situation. Therefore, it is sometimes not that easy to decide when execution of an optimization algorithm should be terminated. There are many different mechanisms can be used for the detection of an appropriate time for ending an optimization run and one of the commonly used mechanism is the setting of a maximum number of generation. The GA procedure is repeated until the maximum number of generation set in the algorithm (which may be adjusted).
ADAPTIVE MUTATION PROBABILITY
Adaptation of operator probabilities is an attempt to make the Genetic Algorithm a more effective optimizer. In this study, we compare the performance of several schemes of adaptive mutation probability as follows:
Mutation probability is random numbers in the range of [pmmin, pmmax]: Mutation probability is dynamically changed in the range of [0.001, 0.05] during the generations.
Adaptive mutation probability based on PDM: Lee and Takagi (1993) propose two Phenotypic Diversity Measure (PDM) performance measures:
PDM1 and PDM2 belong to the interval [0, 1]. If they are near to 1, convergence has been reached, whereas if they are near to 0, the population shows a high level of diversity.
Adaptive mutation probability based on Euclidean distance: Herrera and Lozano (1996) proposed Genotypic Diversity Measure (GDM) based on Euclidean distances of the chromosomes in the population from the best one. The GDM is denoted by ED.
where, , ![]() , dmin = min{d(Cbest, Ci)}Ci is chromosome in population with Euclidean distance
, dmin = min{d(Cbest, Ci)}Ci is chromosome in population with Euclidean distance ![]() . The range of ED is [0, 1]. If ED is low, most chromosomes in the population are concentrated around the best chromosome and so convergence is achieved.
. The range of ED is [0, 1]. If ED is low, most chromosomes in the population are concentrated around the best chromosome and so convergence is achieved.
Lee and Takagi (1993) and Herrera and Lozano (1996) were proposed the use of Fuzzy Logic Controller to dynamically control the mutation probability. But in this study we rather use simple linear formula of pm = PDM1 or pm = PDM2 and pm = 1-ED. These formula are used since the value of PDM1, PDM2 and ED are in the range of [0, 1] as the mutation probability. The nearer to the convergence is shown by higher PDM1, higher PDM2 (nearer to 1) and lower ED (nearer to 0) that each requires higher pm, higher pm and lower pm, respectively. But since we attempt to compare performance of algorithms, we have considered that these techniques should handle the same range of possible pm values in the range of [0.001, 0.1]. So, a transformation was made from the interval considered by these techniques into [0.001, 0.1]. Beside the above measures, we also propose new adaptive mutation probability as below.
Adaptive mutation probability based on Lr distance: Another diversity measure is provided which is based on Lr distance that usually used to measure dissimilarity between two objects. Formula is proposed by Herrera and Lozano (1996) by substituting the ED with LD where Lr distance between two objects is. Then pm = 1-LD.
RESULTS AND DISCUSSION
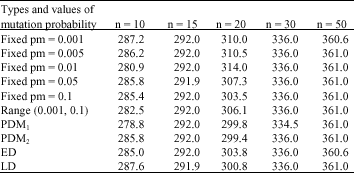
Table 1 shows the result obtained based on performance: average of the best fitness function found at the end of each run. We executed all the algorithms for 10 times and 50 iterations for each run.
Regarding to the GA versions under fixed pm values, we may underline fact that the best performance measures for each problem set are reached with different pm values:
| For n = 10 | : | pm = 0.01 |
| For n = 15 | : | pm = 0.05 |
| For n = 20 | : | pm = 0.1 |
| For n = 50 | : | pm = 0.001 |
whereas, for n = 30, the result of all fixed pm values are the same.
Now, considering the performance between fixed versus adaptive mutation probability, we may observe that adaptive algorithms leads in better solution quality rather than fixed parameter, since for each problem set, it returns results that better than all fixed pm values, or the same as the ones of the most successful GAs with fixed pm settings (the case of n = 15 and n = 50). The adaptive scheme plays a role in improving solution quality and possibly directing search to unknown regions to avoid being trapped in local optimum. By using the adaptive GA, the amount of time to spend in finding appropriate mutation probability values of GA can be reduced.
From the results it can also be deduced that different AGAs are better suited to different problem sets. Compare to other adaptive schemes, PDM1 showed superiority since it can find best performance measure for 2 (two) problem set, while if we compare it to fixed pm, the lowest values of VRPSD objective function from PDM1 were still lower than that can be resulted from all fixed pm setting, or the same with fixed pm results like in the case of n = 15. The proposed LD measure was proven to yield best performance measure among other diversity measure on the problem set n = 15, its performance was also quite good on the n = 20, 30 and 50 but performs worst in n = 10.
| Table 1: | Performance of fixed parameter vs adaptive GA |
 | |
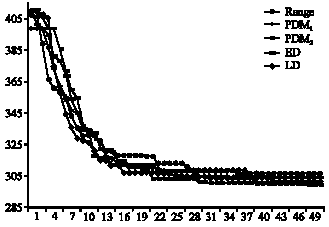 | |
| Fig. 2: | Search process of several AGAs in n = 20 |
The illustration of search process of several adaptive GAs on problem set n = 20 is shown in Fig. 2. It is observed that PDM2 was better than the others and had nearly the same convergence with PDM1 and LD after 40 iterations.
CONCLUSIONS
A Genetic Algorithm (GA) approach as a solution to the VRP with Stochastic demands under restocking policy was designed and presented. The GA does exhibit a very good performance when suitable combinations of operator parameters were used. The amount of time required to examine several combinations of parameters especially in mutation probability can be reduced significantly by using the proposed adaptive mutation probability scheme. When compared with the solution generated using fixed pm values, the adaptive GA does produce a better solution quality. On the other hand, based on the different performances of the various AGAs, it was found that different adaptation mechanisms are better suited to different problems. Future work should be directed towards the development of other adaptive scheme that allows for the integration of these diversity measures with the fitness of every individual.
ACKNOWLEDGMENTS
The research is supported by IRPA Grant Vote No. 74285 from Ministry of Science, Technology and Innovation (MOSTI), Malaysia. The authors would like to thank MOSTI, Research Management Centre (RMC) and Universiti Teknologi Malaysia. The authors also wish to thank lecturers and friends for many helpful ideas and discussion. We also wish to thank Perniagaan Zawiyah Sdn. Bhd. Johor Bahru, Malaysia for providing necessary data in this study.
REFERENCES
- Bertsimas, D.J., P. Chervi and M. Peterson, 1995. Computational approaches to stochastic vehicle routing problems. Transportation Sci., 29: 342-352.
CrossRefDirect Link - Bianchi, L., M. Birattari, M. Chiarandini, M. Manfrin and M. Mastrolilli et al ., 2004. Metaheuristics for the vehicle routing problem with stochastic demands. Parallel Problem Solving from Nature-PPSN VIII, Lect. Notes in Comput. Sci., Vol. 3242, December 16, 2004, Springer, Berlin/Heidelberg, pp: 450-460.
CrossRef - Chepuri, K. and T. Homem-de-Mello, 2005. Solving the vehicle routing problem with stochastic demands using the cross-entropy method. Ann. Operat. Res., 134: 153-181.
CrossRef - De-Falco, I., A.D. Cioppa and E. Tarantino, 2002. Mutation-based genetic algorithm: Performance evaluation. Applied Soft Comput., 1: 285-299.
CrossRefDirect Link - Gendreau, M., G. Laporte and R. Seguin, 1995. An exact algorithm for the vehicle routing problem with stochastic demands and customers. Transportation Sci., 29: 143-155.
CrossRefDirect Link - Holland, J.H., 1992. Adaptation in Natural and Artificial System. 1st Edn., The MIT Press, USA., ISBN-10: 0262581116.
Direct Link - Jerald, J., P. Asokan, R. Saravanan and A.D.C. Rani, 2006. Simultaneous scheduling of parts and automated guided vehicles in an FMS environment using adaptive genetic algorithm. Int. J. Adv. Manuf. Technol., 29: 584-589.
CrossRefDirect Link - Laoufi, 2006. Adapting probabilities of crossover and mutation in genetic algorithms for power economic dispatch. Int. J. Applied Eng. Res., 1: 393-408.
Direct Link - Liu, D.P. and S.T. Feng, 2004. A novel adaptive genetic algorithms. Proceedings of the 3rd Conference on Machine Learning and Cybernetics, August 26-29, 2004, Shanghai, Republic of China, pp: 414-416.
CrossRef - Mei-Yi, L., C. Zi-Xing and S. Guo-Yun, 2004. An adaptive genetic algorithm with diversity-guided mutation and its global convergence property. J. Cent. South Univ. Tec., 11: 323-327.
CrossRefDirect Link - Prins, C., 2004. A simple and effective evolutionary algorithm for the vehicle routing problem. Comput. Operat. Res., 31: 1985-2002.
CrossRefDirect Link - Reeves, C.R., 1995. A genetic algorithm for flowshop sequencing. Comput. Operat. Res., 22: 5-13.
CrossRef - Secomandi, N., 2001. A rollout policy for the vehicle routing problem with stochastic demands. Operat. Res., 49: 796-802.
CrossRefDirect Link - Secomandi, N., 2003. Analysis of a rollout approach to sequencing problems with stochastic routing applications. J. Heuristics, 9: 321-352.
CrossRefDirect Link - Srinivas, M. and L.M. Patnaik, 1994. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybernet., 24: 656-667.
Direct Link - Sugisaka, M. and X. Fan, 2001. Adaptive genetic algorithm with a cooperative mode. Proceedings of the International Symposium on Industrial Electronics, June 12-16, 2001, Pusan, Korea, pp: 1941-1945.
CrossRef - Xing, Y., Z. Chen, J. Sun and L. Hu, 2007. An improved adaptive genetic algorithm for job-shop scheduling problem. Proceedings of the 3rd International Conference on Natural Computation, August 24-27, 2007, Prague, Czech Republic, pp: 287-291.
CrossRef - Yang, W.H., K. Mathur and R.H. Ballou, 2000. Stochastic vehicle routing problem with restocking. Transportat. Sci., 34: 99-112.
Direct Link - Oliver, I.M., D.J. Smith and J.R.C. Holland, 1987. A study of permutation crossover operators on the traveling salesman problem. Proceedings of the 2nd International Conference on Genetic Algorithms, July 28-31, 1987, USA., pp: 224-230.
Direct Link








