Research Article
A Pseudo-Characteristic Based Method for Incompressible Flows with Heat Transfer
Faculty of Mechanical Engineering, University of Tabriz, Iran
S.E. Razavi
Faculty of Mechanical Engineering, University of Tabriz, Iran
During the past decade, much progress has been made in developing computational techniques for predicting flow and heat transfer fields. The accuracy and efficiency of these methods can be affected by factors such as flux treatment, boundary conditions and the grid type. Many existing methods have been developed to solve the compressible flow equation within transonic Mach numbers. However, a lot of applied problems are inherently incompressible and must be treated appropriately. Even with the high interest in incompressible flows, the incompressibility requirement has always been an obstacle in solving the flow equation in a straightforward manner. Since there is no time-evolution term in the continuity equation, the standard time-discretizing schemes developed for solving the compressible Navier-Stokes equations can not be applied directly and the continuity equation imposes a constraint which the momentum equations have to satisfy.
One of the methods which is used for incompressible flows is called pressure correction method. This method uses a Poisson equation for the pressure field (Tsui and Pan, 2006). The other known method is stream function-vorticity which calculates the values of the stream function and vorticity and determines the velocity and pressure fields afterwards (Anderson et al., 2006).
With the progress in recent years of the compressible flow schemes, these schemes have been considered for use with incompressible flows, simply by lowering the Mach number to minimize the compressibility effects. Unfortunately, as Mach number is decreased toward incompressible limit, the performance of compressible methods, in terms of both convergence rate and accuracy suffers greatly. Guillard and Viozart (1999) have identified that, in the low Mach number limit, the discretized solution of the compressible fluid flow equations may fail to provide an accurate approximation to the incompressible equations.
To overcome the difficulties associated with the use of compressible methods, excellent progress has been made in applying Artificial Compressibility Method (ACM) to incompressible flows. ACM, a way of extending the use of compressible flow schemes for near zero Mach number flows, was first introduced by Chorin (1967). This method introduces a pseudo time-derivative of pressure into the continuity equation. This pseudo term changes the mathematical character of the continuity equation from elliptic to hyperbolic. This enables the system of equations to be solved with a variety of schemes developed for compressible flow equations. The method has been successfully used for both steady and unsteady flows. Tai et al. (2004) developed a method to solve Navier-Stokes equations, for velocity field, based on the artificial compressibility method in finite-volume discretization. Tang and Sotiropoulos (2007) applied the ACM to unsteady problems with a kind of fractional time stepping procedure on non-staggered grids. Some researchers have applied ACM in conjunction with different upwind-differencing schemes and solution techniques to solve steady-state as well as unsteady incompressible problems. The upwind-differencing schemes that have been used include the Monotone Upstream-centered Scheme for Conservation Laws (MUSCL) (Rahman and Siikonen, 2001), Total Variation Diminishing (TVD) (Choi et al., 2007), Essentially Non-Osilatiory (ENO) (Cheng and Shu, 2007) and Weighted Essentially Non-oscillatory (WENO) (Yang et al., 1998; Choi et al., 2007) schemes. Kao and Yang (2007) have used a segregated finite-difference scheme based on ACM to solve velocity field of shear-driven cavity. Bassi et al. (2006) have used Discontinuous Galerkin (DG) methods in conjunction with (ACM) to solve incompressible Navier-Stokes equations. As Madsen and Schaffer (2006) have claimed, the time marching approach used in this study can predict both steady and unsteady flows, but this work will focus on steady condition.
The purpose of the current study is the development of characteristic-based methods for velocity and temperature fields of incompressible flows using methods used for solving compressible flow equations. In the new method artificial compressibility concept was successfully used. To calculate convective fluxes Riemann solver of Roe was used. The required coefficients, for both velocity and temperature fields of artificial compressible flows, were derived. For time-marching, 5th order Runge-Kuta algorithm was utilized because of its wide range of stability. The method was examined by solving velocity and temperature fields over circular cylinder and lid driven cavity and comparing the results by those available in literature. As authors know there is no study in literature which uses this approach to solve both velocity and temperature fields of incompressible flows. Other investigators have used the mentioned characteristic-based method for compressible flows and usually their study were restricted to velocity fields.
Governing equations: The primitive form of the incompressible Navier-Stokes equations in Finite-volume form with artificial compressibility is given as:
(1) |
Where:
 | (2) |
Equation 1 has been non-dimensionalized by the following reference values:
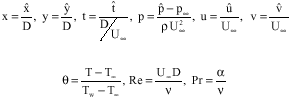 | (3) |
Convective flux treatment: At the present time, various flux treatments are in use. In this study Riemann solver of Roe was applied to calculate fluxes at cell boundaries. By the use of ACM, the governing equations took a hyperbolic dominated nature, therefore the application of characteristic based wave propagation models became possible. Riemann solver of Roe had been originally developed to estimate the fluxes of compressible Euler equations (Roe, 1997) but in current study this solver was applied to the artificial compressible system of Navier-Stokes equations. It can be shown that in this method fluxes at cell boundary can be written as:
(4) |
where, NF is the flux vector normal to the grid boundaries, UR and UL are the values of variables at the right and left side of cell boundaries and
|A| = R|Λ|L | (5) |
where, Λ is a diagonal matrix whose elements are the eigen-values of flux jacobian matrix A and are given by
λ1 = N λ2 = N λ3 = N+ c λ4 = N-c | (6) |
Where:
N = nxu = nyv | (7) |
(8) |
R and L are right and left eigenvectors of matrix A, respectively. These matrices for the primitive variables, in the presence of artificial compressibility factor, has been derived as follows:
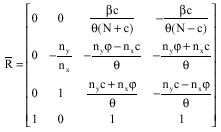 | (9) |
 | (10) |
where, φ is the shear velocity:
φ = nxv-nyu | (11) |
This results lead to the matrix |A|, whose components are:
 | (12) |
All the components were calculated using the average of variables, as follows:
(13) |
The order of accuracy of the scheme depends on choosing UR and UL values. Assigning cell-center values leads to a first order accuracy, eq. 14, but using a kind of interpolation (Drikakis and Rider, 2004) will result in second order of accuracy, eq. 15:
First-order
(14) |
Second-order
(15) |
Viscous fluxes: The viscous fluxes discretization is straightforward and uses 2nd-order averaging. The right hand-side of eq. 1 is approximated by:
 | (16) |
In the calculation of ∂ U/ ∂ x and ∂ U/ ∂ y (Fig. 1), secondary cells are employed.
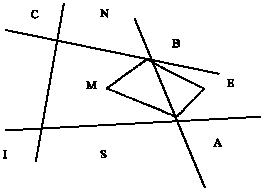 | |
| Fig. 1: | Approximation of viscous fluxes on secondary cells |
∂ U/ ∂ x is approximated as follows:
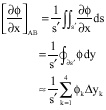 | (17) |
Then:
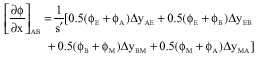 | (18) |
∂U/ ∂ y is calculated in a similar manner. In which s` is the secondary cell area.
Time discretization procedure: For time discretization, 5th-order Runge-Kuta time stepping scheme, because of its wide range of stability (stability margin of CFL = 4 for the linear advective Eq.) and high accuracy, was utilized. This allowed that larger time steps to be chosen, hence allowing a faster convergence to a steady state condition. The solution is updated at consecutive time steps as shown in eq. 19. The proposed characteristic based method was able to dampen oscillations, so no oscillation eliminating method was required.
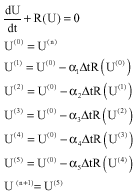 | (19) |
where, ![]() . Stability requirement imposes a restriction on the time steps (Chorin, 1967). To have a stable solution time steps should satisfy the following conditions. By the use of this relation a kind of local time stepping was utilized.
. Stability requirement imposes a restriction on the time steps (Chorin, 1967). To have a stable solution time steps should satisfy the following conditions. By the use of this relation a kind of local time stepping was utilized.
(20) |
Where:
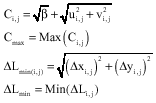 | (21) |
Boundary condition: Consistent boundary treatment ensures the disturbance dissipation in discretized domain without reflection. At the solid boundary a condition of zero mass and energy flux through the surface was prescribed by setting the fluxes corresponding to these faces equal to zero. Pressure on the solid surface was found using a kind of interpolation. Temperature on the solid surface was assumed to be constant. This technique only permits a flux of pressure term of momentum equation through solid boundary. At the inlet boundary pressure was extrapolated from interior domain, velocity and temperature was set equal to the free-stream values. At the outlet boundary the pressure was fixed, remaining variables were interpolated from interior domain.
Grid features: An algebric method was used for grid generation and the grid was clustered near solid boundary. Grid independency is achieved in a 120x120 resolution.
Numerical results: The method was verified by solving flow over a circular cylinder and lid driven cavity. For this flow Pr = 0.71 and CFL = 0.6 was considered. In Fig. 2 Local Nusselt number around circular cylinder is presented and is compared with results of other investigators (Chun and Boehm, 1989). The maximum Nusselt number as expected occurs in the first stagnation point of the cylinder. As boundary layer develops, thermal resistance increases and local Nusselt number reduces. The minimum occurs in separation point.
 | |
| Fig. 2: | Local Nusselt No. over circular cylinder |
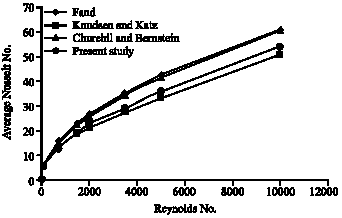 | |
| Fig. 3: | Comparing average Nusselt No. with emprical relations |
In Fig. 3 average Nusslet number against Reynolds Number is compared with empirical relations. Equation 21-23 are proposed, respectively, by Fand, Knudsen and Katz and Churchill and Bernstein (Holman, 2002).
(22) |
(23) |
C and N coefficients for above relation in the range of 40< Re< 4000 are respectively, 0.683 and 0.466.
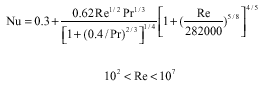 | (24) |
The eq. 22 proposed by Fand, for 10-1<10<105, is simple and has good accuracy. Equation 24 is a little more complex but covers higher Reynolds numbers.
In Fig. 4 streamlines in Re = 200 and Re = 500 are presented. Vorticity region behind the cylinder and unsteady nature of flow is obvious.
It is shown in Fig. 5 that the pressure coefficient at Re = 40 obtained using the proposed method agrees well with that of Choi et al. (2007). In Fig. 6 streamlines for lid driven cavity is compared with the results of Malan et al. (2002) at Re = 1000, 5000.
 | |
| Fig. 4: | Streamlines around circular cylinder |
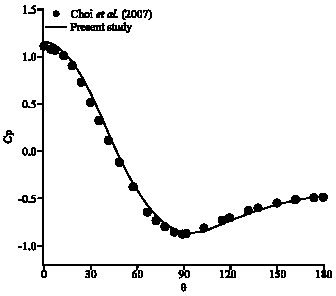 | |
| Fig. 5: | Comparison of wall pressure coefficient along cylinder surface at Re = 40 |
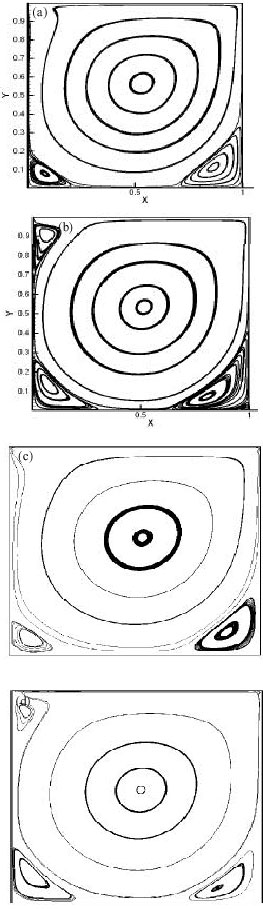 | |
| Fig. 6: | Stream lines for lid driven cavity at Re = 1000, 5000, a and b current study, c and d (Malan et al., 2002) |
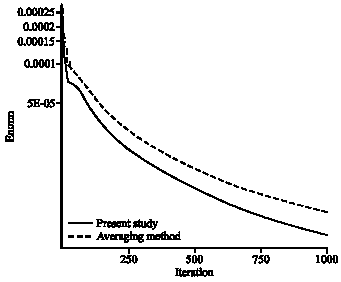 | |
| Fig. 7: | Comparison the convergence rate of proposed method and averaging method, Re =150 |
Error norm is defined as:
(25) |
In the present study a characteristic based method (Riemann solver of Roe) was applied to velocity and temperature fields of incompressible flows. The method was examined by applying it to flow over circular cylinder and shear driven cavity. Artificial compressibility concept made it possible to use the Riemann solver for incompressible flows which is usually used for compressible flows. This method was successful in predicting flows in different Reynolds Numbers. It was able to dampen oscillations, thus generating a stable behavior. This kind of flux treatment relates the physical behavior of flow to the mathematics. The flux treatment considers the Pseudo acoustic wave propagation in the computational domain. This was made possible by reconstruction of fluxes and their corresponding eigenvectors. The comparison of convergence rate of the proposed method and averaging method showed a noticeable reduction in iteration steps.