ABSTRACT
The aim of this study was to provide the modeling research of the nitrogen distribution in onion root zone and leaching the N below the root zone from sandy loam soil. Experiments were conducted with the Research Farm of Bastam Agricultural Center, Shahrood, Iran to investigate the nitrogen distribution pattern under sandy loam soil. The study involved field experiment and modeling of nitrogen leaching. Field data were used to calibrate and validate the solute transport model hydrus-2D. The results of the study can be a great help to onion cultivators in selecting appropriate irrigation and fertigation strategies to minimize the nitrogen leaching and obtain a higher yield. To simulation of nitrogen leaching in soil three fertigation strategies were considered. Results of study revealed that in sandy loam soil, fertigation strategy is effecting the nitrogen leaching. With 2 L h-1 emitter discharge, the N leaching was highest in case of alternate day irrigation-weekly fertigation (strategy B) given 10 min before irrigation cut off. However, at 4 L h-1, N leaching was highest in case of alternate day irrigation-weekly fertigation (strategy A) given 10 min after beginning of the irrigation. This implies that in case of permeable soils like sandy loam, fertigation strategies play role in N leaching. Therefore, while designing drip fertigation system in this soil.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.3157.3165
URL: https://scialert.net/abstract/?doi=jas.2008.3157.3165
INTRODUCTION
The process of application of soluble fertilizer along with irrigation is defined fertigation. Fertigation under drip irrigation is being used commonly for the application of nitrogenous fertilizers in all fruits and vegetable crops. Thompson et al. (2003) carried out field experiment on a sandy loam soil in Southern Arizona with subsurface drip irrigated broccoli determine the effect of N rate and fertigation frequency on crop yield, quality and crop N status and estimate N balance. During one of three season, fertigation frequency affected crop N uptake, but there was no trend of increasing N uptake with increasing fertigation frequency.
Gardenas et al. (2005) investigated nitrate leaching for various fertigation scenarios under micro-irrigation. The effect of fertigation strategy and soil type on nitrate leaching potential for four different micro-irrigation systems was assessed. It was observed that seasonal leaching was the highest for coarse-textured soils.
Chopade et al. (1998) results showed drip fertigation with 50% of the recommended solid fertilizer dose was the best treatment for promoting growth. Peter et al. (2003) studied the fate of nitrogen applied to sugarcane by drip irrigation. It was observed that the high soil water contents maintained with daily application of irrigation water through the drip system promotes mineralization of soil organic mater and hence losses of N to the environment. Jiusheng et al. (2003) observed a uniform distribution of nitrate concentration in the soil in 15 cm around the point source for a given input concentration. A study of solute transport in subsurface drip irrigation was carried out by Cote et al. (2003). The simulation results showed that (1) trickle irrigation can improve plant water availability in medium and low permeability fine-textured to account for their soil hydraulic properties, (2) in highly permeable coarse-texture soils, water and nutrients move quickly downwards from the emitter, making it difficult to wet the near surface zone if emitters are buried too deep and (3) changing the fertigation strategy for highly permeable coarse-texture soils to apply nutrients at the beginning of an irrigation cycle can maintain larger amounts of nutrient near and above the emitter , thereby making them less susceptible to leaching losses. Lafolie et al. (1997) studied modeling of water and nitrogen dynamics in irrigated salad crops. The model used was one-dimensional and is based on Richards` equation for describing saturated- unsaturated water flow in soil. At the soil surface, the model is designed to handle flux-type or imposed pressure boundary conditions.
Hochmuth (2000) developed guidelines from their study for optimum fertilization. The simulations showed the effects of different plant water uptake modeling approaches on water distribution. Simunek et al. (1999) developed the HYDRUS-2D software package for simulating two-dimensional movement of water, heat and multiple solute in variably saturated media.
Delgado et al. (2000) developed the NLEAP model and studied the simulation of nitrate-nitrogen dynamics for cropping systems with different rooting depths. The model was calibrated and validated the potato, lettuce, canola, spring wheat and barley conducted on a similar soil depth. The validated model introduced a new concept of using NLEAP simulations of best management practices for crops with different rooting depths.
A review study of water and solute dynamics under a drip irrigated crop has been done by Mmolawa and Or (2000). It was concluded that water and solute dynamics largely depend on the root distribution and activity of plants as well as nutrient being introduced in the soil root zone.
A simulation model FUSSIM2 was developed by Heinen (2001) for drip fertigation to study various fertigation scenarios. Assouline (2002) compared the effect of three emitter discharges, 0.25, 2.0 and 8 L h-1, on different aspect of the water regime in daily drip irrigated corn, relying on field observations and numerical simulations. The study showed that by changing the fertigation strategy to involve application of non-adsorbed mobile nutrients at the beginning of an irrigation cycle rather than near the end of the cycle, larger amounts of nutrients can be maintained near to and above the drip emitter. Comparison of HYDRUS-2D simulation of drip irrigation with experimental observations was investigated by Skaggs et al. (2004). The result support the use of HYDRUS-2D as a tool for investigating and designing drip irrigation management practices. Many studies have reported that frequent or continuous fertigation of drip-irrigated vegetables is an efficient method of fertigation (Tompson et al., 2003; Ajdary et al., 2007; Halvorson et al., 2002).
The objective of the study was to modeling of the nitrogen distribution in onion root zone and leaching the N below the root zone from sandy loam soil for various irrigation and fertigation strategies using a solute transport model Hydrus-2D. The study involved field experiment and modeling of nitrogen leaching.
MATERIALS AND METHODS
Experimental site: The experiment was conducted in the year 2006 at the Bastam Agricultural Center Farm, Shahrood, Iran which lies the latitudes of 36 °27`33.29” N and longitudes of 54 °58`31.85” E. Climate of Shahrood is categorized as semi-arid, subtropical with hot dry summer and cold winter. The mean annual temperature is 14.4 °C. July and August are the hottest months with 40 years normal maximum temperature of 38 °C. January and February are the coldest months with a mean temperature of -14 ° however, the minimum temperature dips to as low as -5 °C. Area of each plot was 9 m2. Plant to plant and row to row spacing were 15 and 30 cm, respectively. The applied fertilizers were 96 kg ha-1of N, 50 kg ha-1of P and 70 kg ha-1 of K.
In this study to evaluate the physical properties of soil, soil samples were collected from different layers from surface till the depth of 0.9 m and analyzed to determine physical properties. Values of the physical properties such as particle size distribution, bulk density, field capacity, permanent wilting point and hydraulic conductivity are shown in Table 1.
Fertigation schedule: Water requirement of onion crop was estimated using the pan evaporation data. Irrigation was applied on alternate days during the crop growing period based on crop water demand. Irrigation water was applied at the rate of 4 L h-1 through drip emitters placed on the lateral line. Irrigation was stopped two weeks before harvesting to allow the crop to mature. Irrigation interval was 48 h. Total amount of water applied in the entire growing period was 4800 m3 ha-1. Nitrogen fertilizer was applied on weekly basis at the rate of 96 kg ha-1 through drip fertigation in a split doses in the first twelve weeks during growing period.
| Table 1: | Physical properties of soil of the experimental field |
 | |
During each fertigation, fertilizer was applied in the beginning of irrigation for 0.166 h.
Various scenarios considered in the study are given below:
Emitter Discharge rates (L h-1): 2 and 4
Fertigation strategies:
| • | Alternate day irrigation, weekly fertigation, fertigation for 10 min after beginning of irrigation |
| • | Alternate day irrigation, weekly fertigation, fertigation for 10 min before irrigation cutoff |
| • | Daily irrigation, weekly fertigation, fertigation for 10 min before irrigation cutoff |
Field observations: Soil samples were collected from different depths (0-0.15, 0.15-0.30, 0.30-0.45, 0.45-0.60 m) and vertical planes located at emitter and at 10 and 20 cm away from emitter periodically (before fertigation, 2, 12, 24, 48, 96 and 168 h after fertigation) using tube auger from the experimental area to determine spatial and temporal distribution of water and, available nitrogen in the growing season. These were analyzed to determine the gravimetric moisture content and, ammonium and nitrate forms of the available nitrogen. Kjeldahl method (Page et al., 1982) was used to estimate the ammonium and nitrate forms of the available nitrogen.
Nitrogen distribution modeling: Solute transport in soil under surface drip fertigation system is controlled by physical transport. Solute flow is considered to be influenced mainly by soil properties and drip emitter discharge rates. In this study, chemical and biological interactions were not considered. The governing equation for the simulation of the transport of a single non-reactive ion in homogeneous medium in three dimensional axi-symmetrical with polar coordinate system, in advection-dispersion form as given by Bear (1972) and modified by Simunek et al. (1999) by adding nutrient uptake parameter, is as follows:
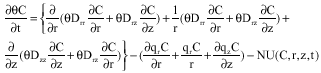 |
where, C [ML-3] is solute concentration in the soil water, qr and qz [LT-1] are the components of the volumetric flux density, Drr, Dzz and Drz [L2T-1] are the components of the dispersion tensor. These components are given by Bear (1972). First term on the right side is solute flux due to dispersion, the second term is solute flux due to convection with flowing water and third term is nutrient uptake by root.
where, |q| [LT-1] is the absolute value of the volumetric flux density, εL and εT [L] are the longitudinal and transversal dispersivities. D0 [L2T-1] is the molecular diffusion coefficient of the solute in free water and τ is the tortuosity factor. The NU term defines the local passive nitrate uptake (ML-3T-1) by plant roots, which is function of space and time and is computed from water uptake value using:
In present study, mineralization gains and denitrification losses sere neglected.
Selection of model: The modeling of nitrogen distribution from the onion field under drip fertigation was carried using the computer simulation model, Hydrus-2D (Simunek et al., 1999). It simulates three-dimensional axially symmetric water flow; solute transport and root water and nutrient uptake based on finite-element numerical solutions of the flow equations. The model can implement a wide range of boundary conditions, irregular boundaries and soil heterogeneities. The software package consists of the HYDRUS-2 computer program and the interactive graphics-based user interface HYDRUS-2D.
Modeling area: Research field was subdivided into identical volume elements with a emitter placed at the surface on the plane of symmetry. Water and nitrogen patterns in the entire field can be described by analyzing the flow in this single volume element irrigated by single emitter. Because of the axial symmetry around the vertical axis, the infiltration process can be viewed as an axi-symmetrical flow with the radius r [L] and the depth z [L] as key variables. In the present study, radius r was taken as 30 cm (half of the lateral to lateral spacing) and depth z as 60 cm. This was done because onion is a shallow rooted crop and nutrient leaching below 60 cm depth will not be available to the plant. The flux radius was taken equal to the wetted radius considering emitter in centre. Figure 1 shows the conceptual diagram of simulated area.
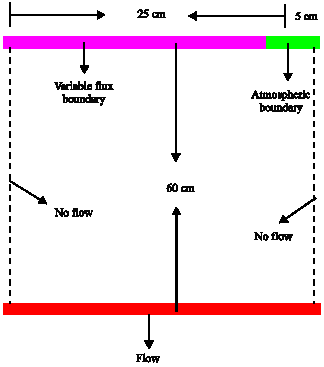 | |
| Fig. 1: | Conceptual diagram of simulated area |
Boundary conditions: In modeling study boundary condition of the modeling area should be clear. Initial available nitrogen concentration as observed in various soil layers within the flow domain was given as initial condition for solute concentration. For all simulations, on the sides of the flow domain, it was assumed that no flow of water and nitrogen took place and hence no-flux boundary condition was chosen, which in Hydrus-2D is specified for impermeable boundaries where, the flux is zero perpendicular to the boundary. In the present study, water table was situated far below the domain of interest and therefore, free drainage boundary condition at the base of the soil profile was considered. Bottom boundary was considered as free drainage boundary.
For simulation of nitrogen distribution in soil layers, Hydrus-2D required input parameters namely saturated water content (θs), residual water content (θr), empirical factors (α, n) and saturated hydraulic conductivity (Ks). Neural Network Prediction option available in Hydrus-2D was used by assigning the values of clay, silt and sand percentage. Saturated hydraulic conductivity of sandy loam was obtained from field experiment. Soils considered for simulation were isotropic. Values of longitudinal and transverse dispersivity were taken as 0.3 and 0.03 cm, respectively. This was confirmed through calibration process. Molecular diffusion was neglected. Values of the hydraulic parameters of the sandy loam soil are presented in Table 2.
| Table 2: | Soil hydraulic parameters for sandy loam soil |
 | |
RESULTS
Calibration and validation of the model: Hydrus-2D was calibrated for prediction of nitrogen distribution in soil with the measured nitrogen in root zone of onion. During calibration runs, simulation period was kept to 168 h, which included one fertigation (for 0.166 h in the beginning of irrigation) and two irrigation events (for 0.33 h at the interval of 48 h). Water flux during each irrigation event was equal to 1.3 cm h-1 and duration of irrigation varied (from 0.33 to 2.5 h) to meet crop water requirement. During fertigation events, duration of nitrogen application was kept equal to 0.166 h however, concentration of solute flux varied 0.253 to 1.35 mg mL-1 depending on the nitrogen applied at various crop growth stages. In validation, simulation period was kept to 36:00 h equal to growing period of onion. Other input parameters were selected in the same was as in case of calibration. Van Genuchten (1980) used analytical model without hysteresis for the soil hydraulic properties. In this study, initial nitrogen concentration in the soil was given as the total available nitrogen, which was considered as sum of NH4+ and NO3– forms of nitrogen. Though the process of nitrification is reduced in saturated zone immediately below the emitter but nitrification occurs in the unsaturated zone around the emitter (Laher and Avnimelech, 1980). Urea was applied as the source of nitrogen which is relatively mobile and is not strongly adsorbed by soil colloids. In soil, urea is hydrolyzed to the ammonium ion and subsequently undergoes to nitrification. Leaching of nitrogen occurs mostly in the nitrate form, which is predicted by model. Therefore, in this study, predicted nitrogen distribution within the root zone and cumulative nitrogen going below root zone are reported as available nitrogen and amount of nitrogen leached.
Figure 2 and 3 show the simulated and observed N concentration at various depths at 2, 4, 24, 48, 96 and 168 h after fertigation. The results reveal that simulated and observed N distributions follow similar trends and N concentration decreases with increasing depth. These Fig. 2 and 3 also reveal that concentration of N at various points decreases with elapsed time after fertigation.
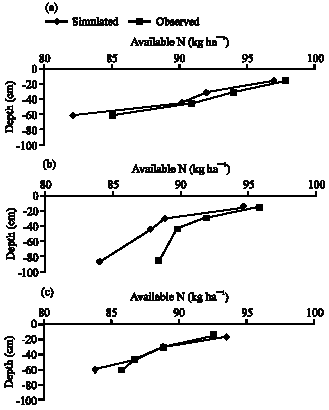 | |
| Fig. 2: | Simulated and observed N concentration at the end of first month after transplanting (a) 2, (b) 4 and (c) 24 h after fertigation |
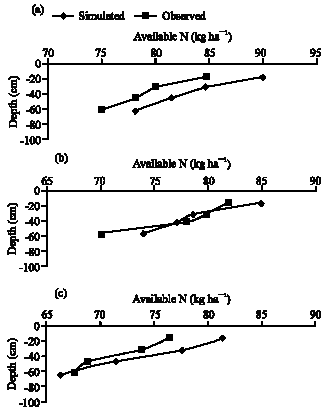 | |
| Fig. 3: | Simulated and observed N concentration at the end of first month after transplanting (a) 48 (b ) 96 and (c) 168 h after fertigation |
| Table 3: | Comparison of simulated and observed N concentration at the end of simulation period (Validation of the model) |
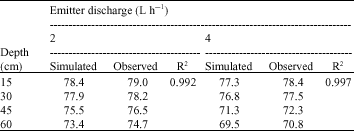 | |
For example, simulated and observed N concentrations below the emitter 4 h after fertigation were 95 and 96 kg ha-1 in the first layer and the same was 94 and 93 kg ha-1 after 24 h. Similar trends were observed in all layers.
To examine the predictability of the model on seasonal basis, simulation was carried out to predict the N distribution at the end of growing season (taking the simulation period of 150 days). The Table 3 reveals that simulated and observed values of N follow similar trend with not much difference. Simulated and observed N concentrations in the soil at the time of harvesting varied from 69.5 to 79.5 kg ha-1. Correlation coefficient between simulated and observed N concentration varied from 0.992 to 0.997. This also indicates that there is not much difference between simulated and observed N concentrations. The above discussion implies that Hydrus-2D can be used to predict the N concentration in the soil under drip fertigation on seasonal basis also with very good predictability. After calibration and validation, model was used to predict the nitrogen distribution and leaching from onion field under drip fertigation system for various scenarios.
Simulation of nitrogen distribution: N distributions in different time after fertigation obtained from the simulations were interpreted to analyze the effect of emitter discharge rates and fertigation strategies on N distribution. Simulation of N distribution in soil was done in vertical and radial direction. Selection of values of input parameters and method of interpretation of the model outputs were done.
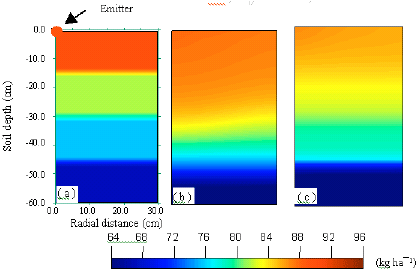
Simulation of N distribution in vertical direction: In this simulation, alternate day irrigation and weekly fertigation schedule was adapted. Figure 4a shows that initial N concentration decreased with depth however, after fertigation with pre-decided schedule, N concentration in the vicinity of emitter, first and second soil layer immediately 4 h after fertigation is increased. The Fig. 4b and c, show that 4 and 24 h after fertigation N concentration in active root zone depth (i.e., middle layer) has increased thereby justifying the use of drip fertigation in maintaining adequate nutrient concentration in this zone.
 | |
 | |
| Fig. 4: | Simulated nitrogen concentration with 4 L h-1 emitter discharge at the end of second month after transplanting (a) Initial, (b) 4 , (c) 24 , (d) 48 , (e) 72 and (f) 96 h after fertigation |
It can also be seen that color spectrum of N concentration in the last layer has not changed much up to 24 h after fertigation. This indicates that N concentration at the end of second month after transplanting in the last layers is nearly same to initial even 24 h after fertigation. This implies that under this scenario, possibility of N leaching is not much. It may be mention that observed N concentration under this scenario is at the end of second month was also in the same range. Color spectrum also revealed that N concentration in the first layer decreased with progress of time after fertigation (Fig. 4d-f). The data shows that difference in N concentration is more at the depth of 0-30 cm which is classified as active root zone. Concentration of N was more at the vertical plane located at 15 cm from emitter. It may be mentioned that plant is located at 15 cm from the emitter and this would also mean adequate N availability near the plant roots.
Figure 5a-c revealed that 5 days after fertigation amount of N in first and second soil layers slowly is decreased and 7 day after fertigation there was lowest N in active crop root zone. Figure 5c showed that 7 day after fertigation, crop needs nutrient and fertigation schedule should be repeated.
Figure 5d-f shows that after next fertigation nitrogen concentration is increasing again in first layer and it is not leaching to down soil layers.
Simulation of N distribution in radial direction: Figure 6 shows simulation of N distribution in radial direction at the depth of 15 cm at the end of 2 month after transplanting with emitter discharge rate of 4 L h-1. This depth was selected because it was assumed that active root zone of onion crop is this zone. It can be observed that N concentration at this depth has not changed in radial direction for a particular soil type. It is observed that N concentration is distributed uniformly in radial distance at this depth for emitter discharge rates of 4 L h-1. Figure 6 also revealed that effect of emitter discharge on N concentration below emitter and at radial direction is more in case of sandy loam soil. Distribution of N concentration indicated that effect of emitter discharge was more in the vicinity of emitter in the upper layer. Effect of discharge on N concentration in the middle and lower layer was not significant.
 | |
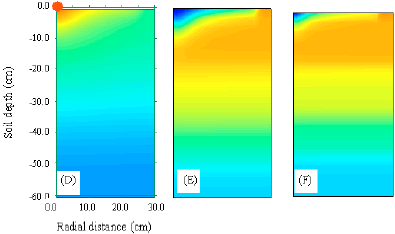 | |
| Fig. 5: | Simulated nitrogen concentration with 4 L h-1 emitter discharge at the end of second month after transplanting (a) 120, (b) 144, (c) 168 after fertigation, (d) 4, (e) 24 and (f) 48 h after next fertigation |
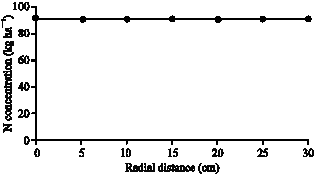 | |
| Fig. 6: | Simulation of nitrogen distribution in radial direction at the depth of 15 cm with 4 L h-1 emitter discharge, second moth after transplanting |
Nitrogen distribution in the soil at the time of harvesting: Color spectrum revealed that at the harvesting time higher concentration of nitrogen is distributed in the first and middle layers in case of sandy loam soil (Fig. 7). This implies that 150 days after transplanting, nitrogen is distributed mostly in upper soil layer and less amount of nitrogen is leached below than the active crop root zone. To examine the leaching potential, N concentration in the last layer can be used as an indicator. Maximum amount of N concentration in this layer for sandy loam soil was 78 kg ha-1.
| Table 4: | Percentage of N leached below than root zone with different fertigation strategy |
 | |
This implies that more permeable soils are prone to leaching compared to the less permeable soils. However, it may be mentioned that N concentration in active root zone is adequate.
Nitrogen leaching below the root zone depth: To find out the leaching potential of sandy loam soil in the end of crop growing period under various emitter discharge rates, amount of N going below 60 cm depth were determined and are shown in Table 4. Amount of N going below the root zone depth was obtained from the cumulative drainage boundary flux component available in post processing files of Hydrus-2D. Nitrogen leaching percentage was taken as ratio of cumulative N going below 60 cm depth and applied N.
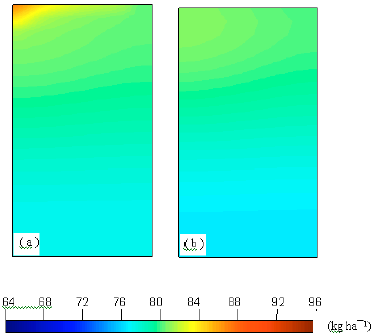 | |
| Fig. 7: | Simulated nitrogen concentration at the time of harvesting with emitter discharge of (a) 2 L h-1 and (b) 4 L h-1) |
The table revealed that in all cases percentage of N leached below the root zone depth was much less. N leaching increased with increase in discharge rate under all fertigation strategies for sandy loam soil. For the same soil with 2 L h-1 emitter discharge, the N leaching was highest in case of alternate day irrigation-weekly fertigation (strategy B ) given 10 min before irrigation cut off. However, at 4 L h-1, N leaching was highest in case of alternate day irrigation-weekly fertigation (strategy A ) given 10 min after beginning of the irrigation. This implies that in case of permeable soils like sandy loam, fertigation strategies play role in N leaching. Therefore, while designing drip fertigation system in this soil, above discussion should be considered.
DISCUSSION
Results of this study showed that emitter discharge played a significant role in influencing N concentration in middle and lower layers for sandy loam soil. However, in case of 2 and 4 L h-1 emitter discharge, N concentration in the active root zone (i.e., middle layer) is comparatively more. Though, N concentrations for 2 and 4 L h-1 in the middle layer (i.e., in active root zone) are adequate, leaching percentages of N below 60 cm will be more for the discharge of 4 L h-1. This may be due to the fact higher emitter discharge may have pushed the N below the 60 cm.
Table 4 revealed that N leaching increased with increase in discharge rate under all fertigation strategies for sandy loam soil. For the same soil with 2 L h-1 emitter discharge, the N leaching was highest in case of alternate day irrigation-weekly fertigation (strategy B ) given 10 min before irrigation cut off. However, at 4 L h-1, N leaching was highest in case of alternate day irrigation-weekly fertigation (strategy A ) given 10 min after beginning of the irrigation. This implies that in case of permeable soils like sandy loam, fertigation strategies play role in N leaching. Therefore, while designing drip fertigation system in this soil, above discussion should be considered.
CONCLUSION
Results presented in this study showed that if the drip system designs properly, it will distribute uniformly nutrient in radial and vertical direction of soil surface. Calibration and validation results show that Hydrus-2D can be used for simulation of water and nitrogen distribution and nutrient leaching in soil. Results revealed that in the one week fertigation schedule adequate amount of nitrogen was available in onion root zone. Results also revealed in sandy loam soil fertigation strategy is effecting the nitrogen leaching. N leaching increased with increase in emitter discharge rate under all fertigation strategies. With 2 L h-1 emitter discharge, the N leaching was highest in case of alternate day irrigation-weekly fertigation (strategy B ) given 10 min before irrigation cut off. However, at 4 L h-1, N leaching was highest in case of alternate day irrigation-weekly fertigation (strategy A ) given 10 min after beginning of the irrigation. This implies that in case of permeable soils like sandy loam, fertigation strategies play role in N leaching. Therefore, while designing drip fertigation system in this soil, above discussion should be considered.
ACKNOWLEDGMENTS
I acknowledge Dr. D.K. Singh, A.K. Singh and Manoj Khanna Water Technology Center , Indian Agricultural Research Institute, New Delhi-India. I am thankful Mr. Hassan Goley Irrigation Engineer, Shahrood University of Technology , Shahrood. Iran, for his helps in study work.
REFERENCES
- Assouline, S., 2002. The effect of microdrip and conventional drip irrigation on water distribution and uptake. Soil Sci. Soc. Am. J., 66: 1630-1636.
Direct Link - Chopade, S.O., P.N. Bansode and S.S. Hiwase, 1999. Studies on fertilizer and water management to onion. PKV Res. J., 22: 44-46.
Direct Link - Cote, C.M., K.L. Bristow, P.B. Charlesworth, F.J. Cook and P.J. Thorburn, 2003. Analysis of soil wetting and solute transport in subsurface trickle irrigation. J. Irrig. Sci., 22: 143-156.
CrossRefDirect Link - Delgado, J.A., R.F. Follett and M.J. Shaffer, 2000. Simulation of nitrate-nitrogen dynamics for cropping systems with different rooting depths. Soil. Sci. Soc. Am. J., 64: 1050-1054.
Direct Link - Gardenas, A.I., J.W. Hopmans, B.R. Hanson and J. Simunek, 2005. Two-dimensional modeling of nitrate leaching for various fertigation scenarios under micro-irrigation. Agric. Water Manage., 74: 219-242.
CrossRefDirect Link - Halvorson, A.D., R.F. Follett, M.E. Bartolo and F.C. Schweissing, 2002. Nitrogen fertilizer use efficiency of furrow-irrigated onion and corn. Agron. J., 94: 442-449.
CrossRefDirect Link - Li, J., Z. Jianjun and L. Ren, 2003. Water and nitrogen distribution as affected by fertigation of ammonium nitrate from a point source. Irrigation Sci., 22: 19-30.
CrossRefDirect Link - Lafolie, F., L. Bruckler, A.M. de Cockborne and C. Laboucarie, 1997. Modeling the water transport and nitrogen dynamics in irrigated salad crops. Irrig Sci., 17: 95-104.
CrossRefDirect Link - Laher, M. and Y. Avnimelech, 1980. Nitrification inhibition in drip irrigation systems. Plant Soil, 55: 35-42.
CrossRefDirect Link - Peter, J.T., F.J. Cook and K.L. Bristow, 2003. Soil-dependent wetting from trickle emitters: Implications for system design and management. Irrig. Sci., 22: 121-127.
CrossRefDirect Link - Skaggs, T.H., T.J. Trout, J. Simunek and J. Shouse, 2004. Comparison of HYDRUS-2D simulation of drip irrigation with experimental observations. J. Irrig. Drain. Eng., 130: 1-7.
CrossRefDirect Link - Thompson, T.L., S.A. White, J. Walorth and G.J. Sower, 2003. Fertigation ferquency for subsurface drip-irrigated Broccoli. Soil. Sci. Soc. Am. J., 67: 910-918.
Direct Link - Van Genuchten, M.T., 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J., 44: 892-898.
CrossRefDirect Link








