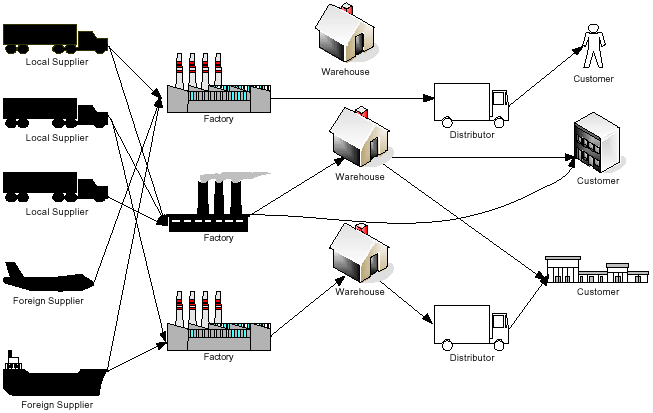
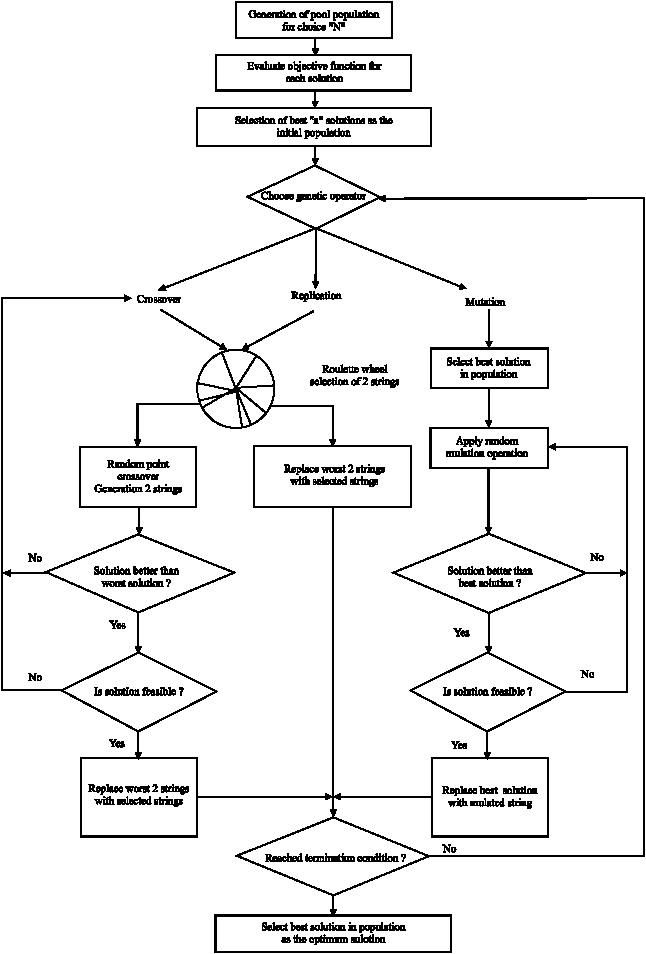
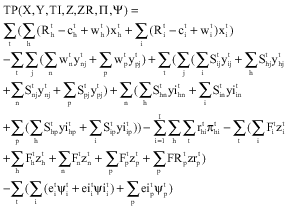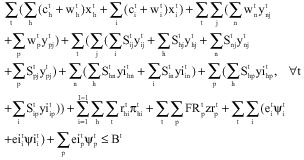Research Article
A Genetic Approach to Optimize Mathematical Model of Facilities Relocation Problem in Supply Chain
Department of Industrial Engineering, Mazandaran University of Science and Technology, Babol, Iran
H. Fazlollahtabar
Young Researchers Club, Islamic Azad University, Babol Branch, Iran
D. Shafiei
Vice President of Small Industries at Mazandaran Industrial Parks Corporation, Sari, Iran