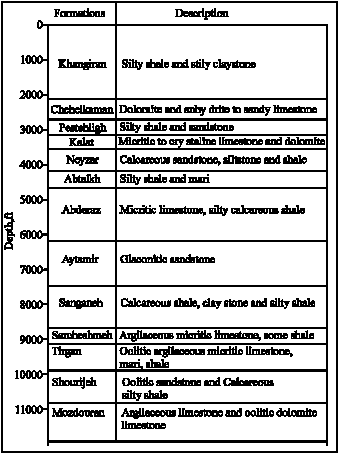
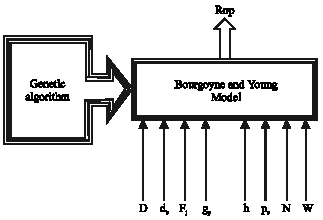
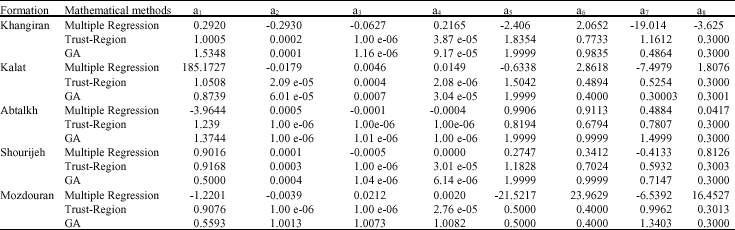
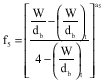Research Article
Determining Bourgoyne and Young Model Coefficients Using Genetic Algorithm to Predict Drilling Rate
Ferdowsi University of Mashhad, Mashhad Iran
A. Bahari
National Iranian Oil Company (NIOC), Iran
F. Nejati Moharrami
Ferdowsi University of Mashhad, Mashhad Iran
M.B. Naghibi Sistani
Ferdowsi University of Mashhad, Mashhad Iran