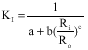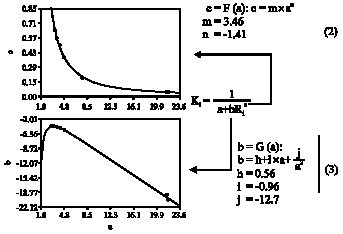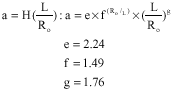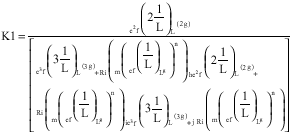Research Article
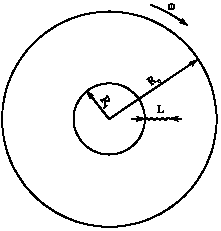
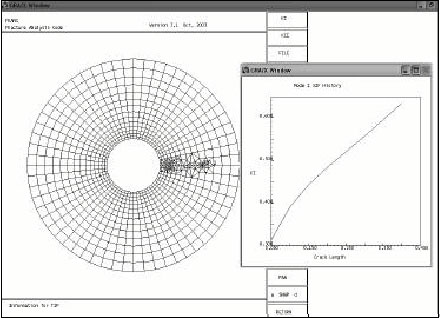
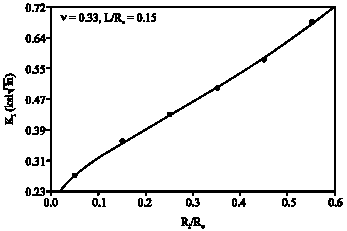
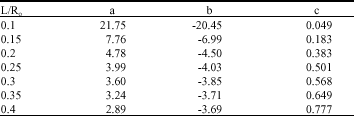
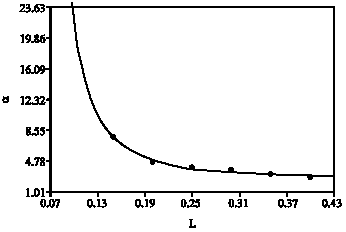
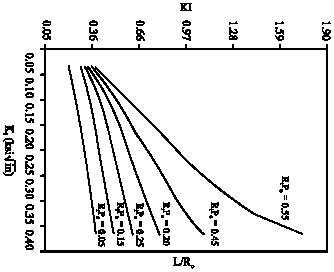
Calculation of Stress Intensity Factor by Algebraic Emulator Based on Statistical Resultants of FRANC2D in Rotary Cracked Disks
Department of Mechanical, Shahrood University of Technology, Daneshgah Blvd. Shahrood, Isalmic Republic of Iran
E. Mohammadia
Department of Mechanical, Shahrood University of Technology, Daneshgah Blvd. Shahrood, Isalmic Republic of Iran
M. Mahdizaseh Rokhia
Department of Mechanical, Shahrood University of Technology, Daneshgah Blvd. Shahrood, Isalmic Republic of Iran