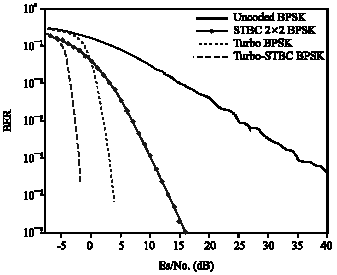
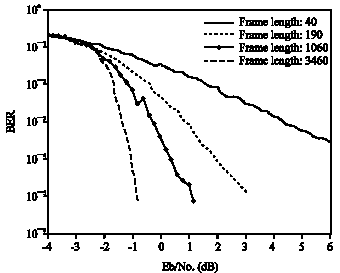
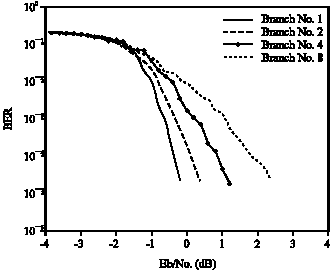
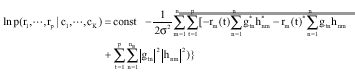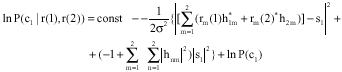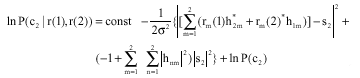Research Article
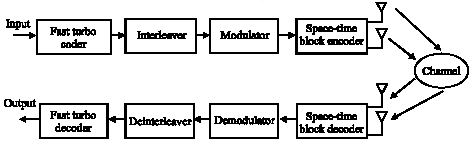
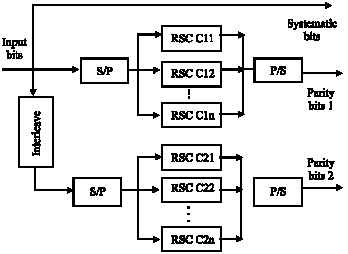
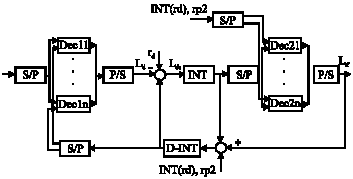
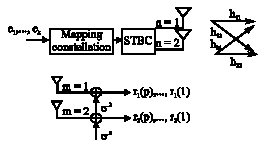
Fast Turbo Codes Concatenated With Space-Time Block Codes
Department of Electrical Engineering, KN Toosi University of Technology, P.O. Box 16315-1355, Tehran, Iran
Mehrdad Ardebilipour
Department of Electrical Engineering, KN Toosi University of Technology, P.O. Box 16315-1355, Tehran, Iran
Abolfazl Razi
Department of Electrical Engineering, KN Toosi University of Technology, P.O. Box 16315-1355, Tehran, Iran