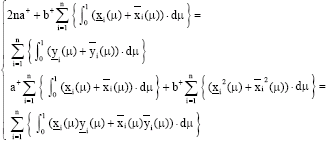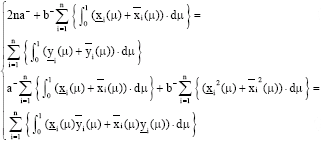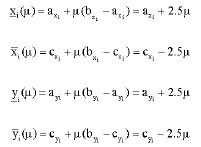Research Article
Rainfall-Runoff Modeling Using Fuzzy Methodology
Department of Hydraulic Structures, Department of Mining Engineering, Shahid Bahonar University of Kerman, Iran
H.R. Khatami
Department of Mining Engineering, Shahid Bahonar University of Kerman, Iran
M.T. Moeti
Bakhtar Regional Electric Company, Arak, Iran
G. Barani
Department of Civil Engineering, Shahid Bahonar University of Kerman, Iran









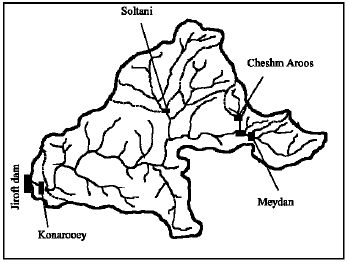
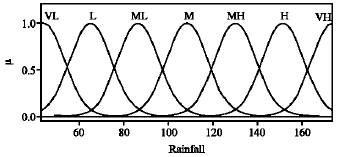

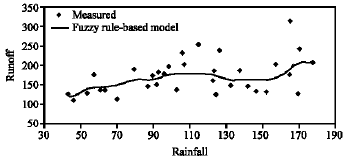
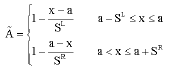
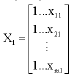 in the model. Thus the problem is:
in the model. Thus the problem is: