Research Article
A Hybrid Method of Neural Networks and Genetic Algorithm in Econometric Modeling and Analysis
Department of Industrial Engineering, Sharif University of Technology, P.O. Box 11155-9414, Azadi Ave., Tehran, Iran
Seyed Taghi Akhavan Niaki
Department of Industrial Engineering, Sharif University of Technology, P.O. Box 11155-9414, Azadi Ave., Tehran, Iran









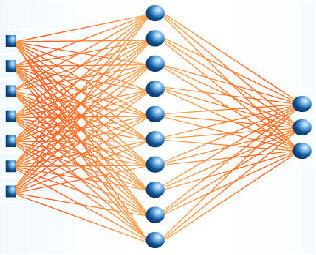
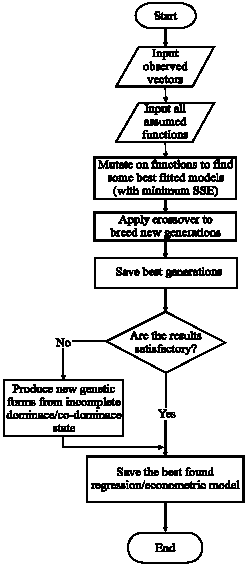
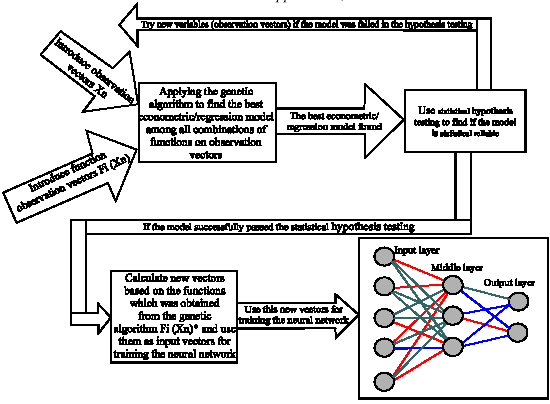

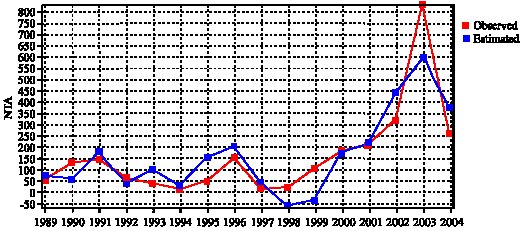
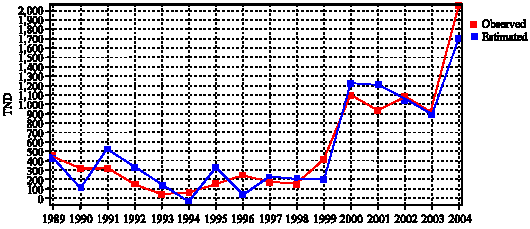
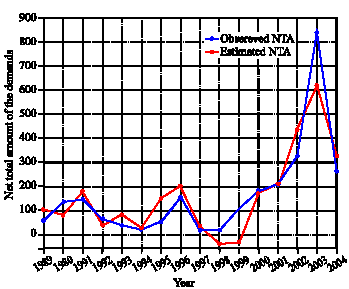

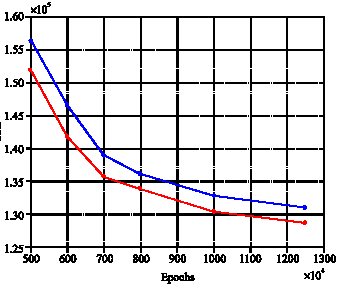
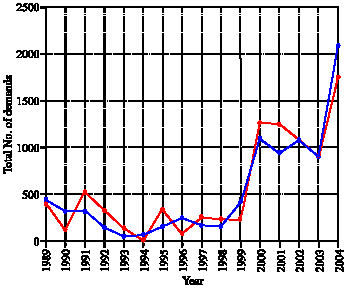

Seyed Taghi Akhavan Niaki Reply
How come when I search Scopus for the author either "Akhavan Niaki" or "Hasheminia" this paper does not appear?