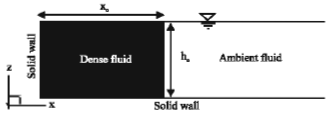
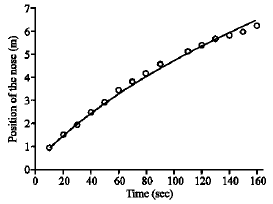
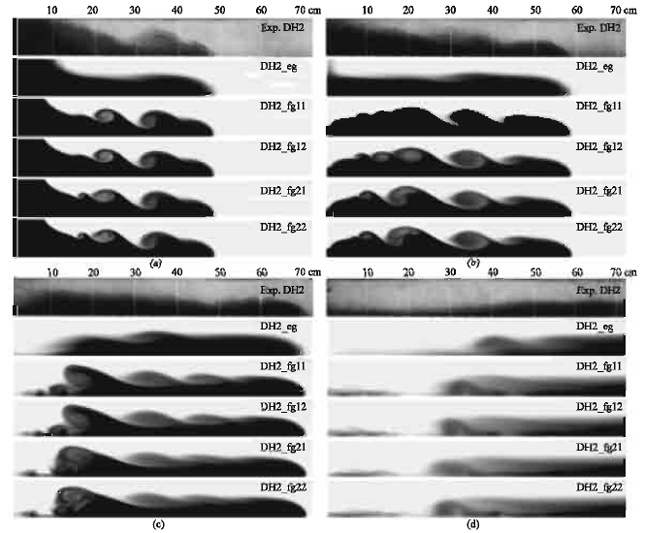
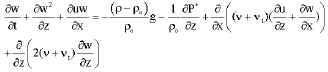Research Article
URANS Simulation of 2D Continuous and Discontinuous Gravity Currents
Tarbiat Modares University, Tehran, Iran
M.M. Namin
University of Tehran, Tehran, Iran
S.A.A. Salehi
Tarbiat Modares University, Tehran, Iran
B. Firoozabadi
Sharif University of Technology, Tehran, Iran
M. Javan
Razi University, Kermanshah, Iran