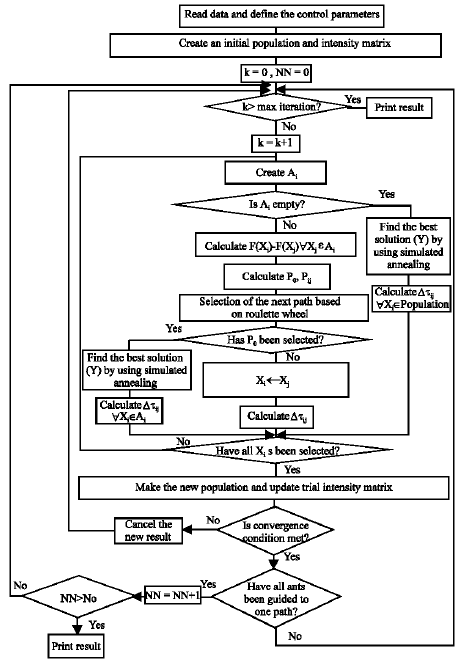
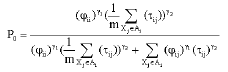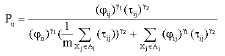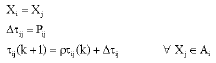Research Article
A Hybrid Evolutionary Algorithm Based on ACO and SA for Cluster Analysis
Department of Electronic and Electrical, Shiraz University of Technology,Modars Blvd. Shiraz, Iran
J. Olamaei
Islamic Azad University, South Tehran-Barnch, Tehran, Iran
B. Amiri
Department of Information Technology and Computer Engineering, Fars Science and Research Branch of Islamic Azad University, Shiraz, Iran