Research Article
Computation of Surface Roughness of Mountains Extracted from Digital Elevation Models
Science and Technology Research Institute for Defense (STRIDE),Ministry of Defense, Malaysia
In the past few decades, the quantitative computation of surface roughness has received increasing attention due to its importance in numerical surface study. A number of algorithms have been employed to compute surface roughness; a summary can be found in Shepard et al. (2001) and Li et al. (2005). The most commonly used roughness parameter and the easiest to obtain, is the Root-Mean-Square (RMS) height, or the standard deviation of heights above the mean (Brock, 1983). The profile is first detrended by subtracting a best fit linear function from the data, leaving a series of heights with a mean value of zero. This approach is insensitive to amplitude differences and is not a good frequency discriminator. An alternative approach is to fit a plane to a surface and use the error as an estimate of the surface roughness (Wilcox and Gennery, 1987). In the case of two sinusoidal surfaces of differing frequencies, plane fitting suffers from a fundamental shortcoming by producing the same roughness estimation. Stone and Dugundji (1965) propose a method of computing surface roughness using Fourier analysis. This method measures roughness along specific directions of a surface and includes amplitude, frequency and autocorrelation terms. This approach provides surface roughness parameters that have consistent representation in the frequency domain. However, as it depends on the direction of measurement, it is influenced by the rotation and translation of the surface. The slope and intercept of the logarithmic plot of the power spectrum of the terrain profile is reported as a roughness parameter by van Zyl et al. (1991). However, there is no simple correspondence between the intercept or the slope of the logarithmic plot of the power spectrum and commonly used roughness measures. Other reported roughness measures, developed to overcome these shortfalls, include effective slope (Miller and Parsons, 1990; Campbell and Garvin, 1993), autocorrelation length (Turcotte, 1997), radiosity models (Li et al., 1998), median and absolute slope (Kreslavsky and Head, 1999), granulometry (Tay et al., 2005a) and high-order statistics (Nikora, 2005). These algorithms, which operate at singular scales of measurement, provide scale-dependant roughness parameters.
Dinesh (2007a) proposes a procedure to compute a scale-independent surface roughness parameter from Digital Elevation Models (DEMs). First, multiscale DEMs are generated using the lifting scheme. The area of pixels modified at each scale is computed. The computed areas are divided with the area of the DEM to obtain the normalized probability functions, which are used to compute the average size of convex and concave regions in the DEM and the scale-independent average roughness of the terrain of the DEM due to the distribution of convex and concave regions in the terrain.
In this study, the procedure proposed in Dinesh (2007a) is extended to perform the computation of surface roughness of individual mountain objects extracted from DEMs.
MATERIALS AND METHODS
The Global Digital Elevation Model (GTOPO30) of Great Basin: The DEM in Fig. 1 shows the area of Great Basin, Nevada, USA. The area is bounded by latitude 38° 15’ to 42° N and longitude 118° 30’ to 115° 30’W. The DEM was rectified and resampled to 925 m in both x and y directions. The DEM is a Global Digital Elevation Model (GTOPO30) and was downloaded from the USGS GTOPO30 website (http://edcwww.cr.usgs.gov/landdaac /gtopo30/gtopo30.html). GTOPO30 DEMs are available at a global scale, providing a digital representation of the Earth’s surface at a 30 arc-seconds sampling interval. The land data used to derive GTOPO30 DEMs are obtained from Digital Terrain Elevation Data (DTED), the 1-degree DEM for USA and the Digital Chart of the World (DCW). The accuracy of GTOPO30 DEMs varies by location according to the source data. The DTED and the 1-degree dataset have a vertical accuracy of ±30 m while the absolute accuracy of the DCW vector dataset is ±2000 m horizontal error and ±650 m vertical error (Miliaresis and Argialas, 2002).
Mountain extraction: Mountains are the portions a terrain that are sufficiently elevated above the surrounding land (greater than 300 to 600 m) and have comparatively steep sides. In a mountain, two parts are distinctive:
| • | The summit, the highest point (the peak) or the highest ridges. |
| • | The mountainside, the part of a mountain between the summit and the foot (Bates and Jackson, 1987). |
The mapping of mountains is generally performed manually through fieldwork and visual interpretation of topographic maps, which is a time consuming and labor intensive activity. In recent times, extraction techniques have evolved from manual through computer assisted to automated methods with DEMs as the input data. In seeking the efficient extraction of mountains from DEMs, various algorithms have been proposed (Graff and Usery, 1993; Miliaresis and Argialas, 1999; Miliaresis, 2000; Dinesh, 2006).
 | |
| Fig. 1: | The GTOPO30 DEM of Great Basin. The elevation values of the terrain (minimum 1005 m and maximum 3651 m) are rescaled to the interval of 0 to 255 (the brightest pixel has the highest elevation). The scale is approximately 1:3,900,00 |
The mountains of the DEM of Great Basin are extracted using the mathematical morphological based algorithm proposed in Dinesh (2006). First, ultimate erosion is performed on the DEM to extract the peaks of the DEM. Conditional dilation is performed on the extracted peaks to obtain the mountains of the DEM. A total of 14 distinct individual mountains objects are extracted from the DEM (Fig. 2).
Generation of multiscale DEMS using the lifting scheme: Feature detection and characterization often need to be performed at different of scales measurement. Wood (1996a, b) shows that analysis of a location at multiple scales allows for a greater amount of information to be extracted from a DEM about the spatial characteristics of a feature. The term scale refers to combination of both spatial extent and spatial detail or resolution (Goodchild and Quattrochi, 1997; Tate and Wood, 2001). A number of research efforts have been conducted to characterize geomorphological features, such as drainage and ridge networks (Radhakrishnan, 2002, 2003, 2004; Sagar et al., 2003; Tay et al., 2005b), catchments (Dinesh, 2007b) and mountains (Dinesh, 2007c,d,e; Dinesh and Fadzil, 2007a,b), using the variation in the spatial extent over which these features are defined.
In this study, multiscaling is performed using the lifting scheme (Sweldens, 1996, 1997). The lifting scheme is a flexible technique that has been used in several different settings, for easy construction and implementation of traditional wavelets
 | |
| Fig. 2: | Extraction of mountains from DEM. (a) The extracted mountains and (b) A total of 14 individual mountains objects are identified using connected component labeling (Pitas, 1993). |
Lifting consists of the following three basic operations:
Step 1: Split: The original data set x[n] is divided into two disjoint subsets, even indexed points xe[n] = x[2n] and odd indexed points x0[n] = x[2n+1].
Step 2: Predict: The odd and even subsets are often highly correlated. This correlation structure typically local and hence, it is possible to accurately predict the wavelet coefficients d[n] as the error in predicting x0[n] from xe[n] using the prediction operator P:
(1) |
Where:
(2) |
Step 3: Update: Scaling coefficients c[n] that represent a coarse approximation to the signal x[n] are obtained by combining xe[n] and d[n]. This is accomplished by applying an update operator U to the wavelet coefficients and adding to xe[n]:
(3) |
Where:
(4) |
These three steps form a lifting stage. The lifting scheme scans 2D images row-by-row. Using a DEM as the input, an iteration of the lifting stage generates the complete set of multiscale DEMs cr[n] and the elevation loss caused by the change of scale dr[n].
Multiscale DEMs of the Great Basin region are generated by implementing the lifting scheme on the DEM of Great Basin using scales of 1 to 20. As shown in Fig. 3, as the scale increases, the merge of small regions into the surrounding grey level regions increases, causing removal of fine detail in the DEM. The fine detail in DEMs represents crenulations, which are used to extract hydrological features from DEMs. Convex crenulations are used to extract ridge networks while concave crenulations are used to extract drainage networks (Gilbert, 1909; Howard, 1994; Rodríguez-Iturbe and Rinaldo, 1997). The distribution of convex and concave regions in a terrain indicates the surface roughness of the terrain. The removal of convex and concave regions from the terrain during the multiscaling process results in the terrain becoming smoother.
The mask of pixels modified at each scale r is identified by computing the difference between the DEM of scale r and the DEM of the previous scale r-1. The resulting image is thresholded into a binary image by converting all pixels with grey level more than 0 to binary 1 and all pixels with grey level 0 to binary 0. The computed masks of pixels modified are shown in Fig. 4.
Computation of surface roughness of individual mountain objects: The procedure proposed to perform the computation of surface roughness of the individual mountain objects is demonstrated using the first mountain object (Fig. 5). The mask of pixels modified in the each mountain object at each scale (Fig. 6) is computed by performing the intersection operation between the mountain object and the mask of pixels modified at each scale.
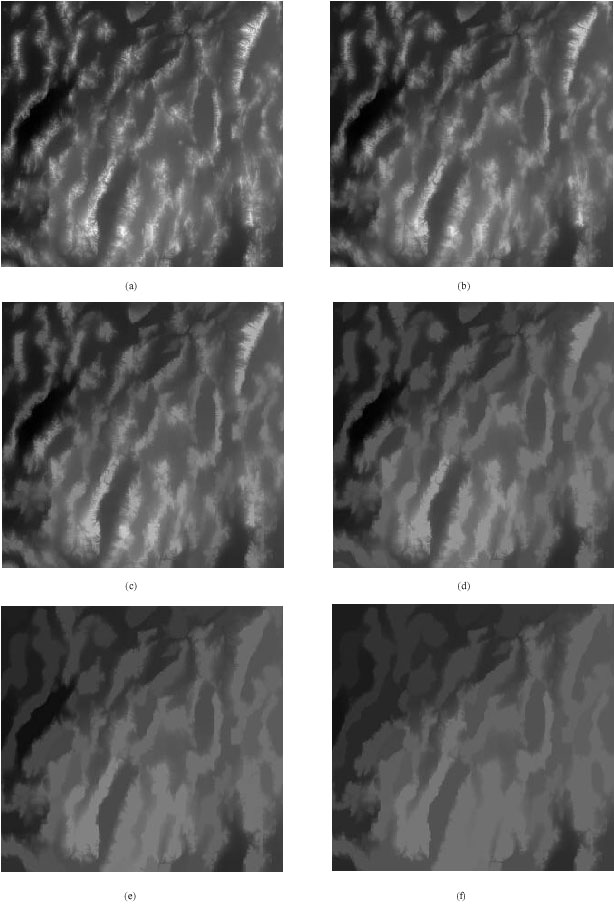 | |
| Fig. 3: | Multiscale DEMs generated using scales of (a) 1 (b) 3 (c) 5 (d) 10 (e) 15 and (f) 20 |
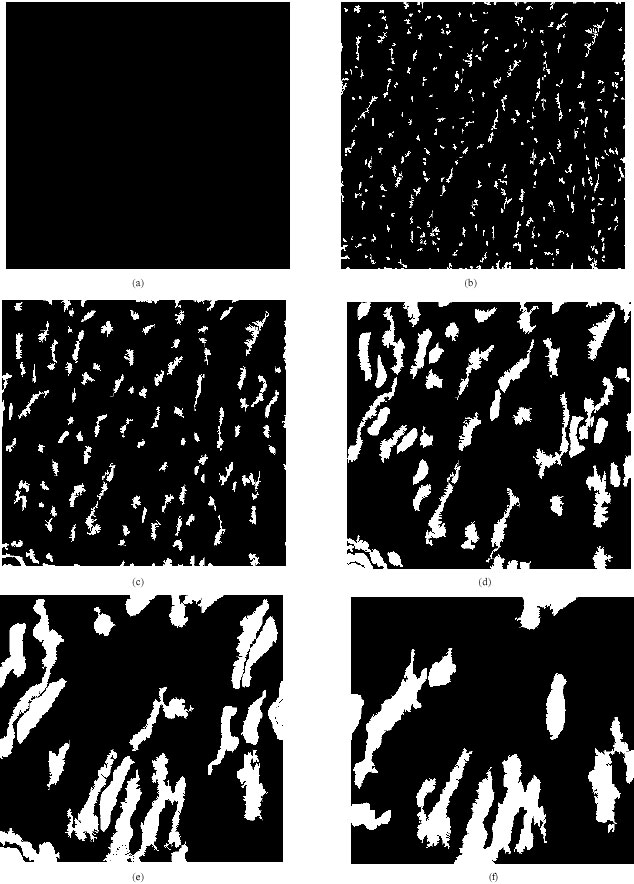 | |
| Fig. 4: | Mask of pixels modified during the multiscaling process for the corresponding multiscale DEMs in Fig. 3. This indicates the convex and convex regions removed from the DEM during the multiscaling process |
 | |
| Fig. 5: | The first mountain object |
 | |
| Fig. 6: | The mask of pixels modified in the first mountain object during the multiscaling process for the corresponding multiscale DEMs in Fig. 3. This indicates the convex and convex regions removed from the mountain object during the multiscaling process |
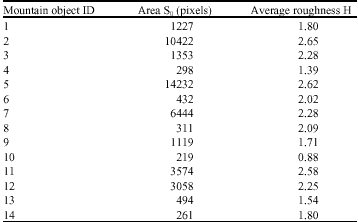
| Table 1: | The computed values of S0 and H for the individual mountain objects |
 | |
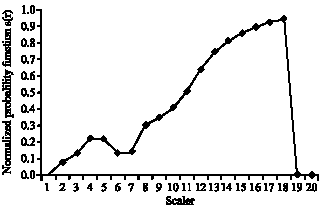 | |
| Fig. 7: | Plot of the normalized probability functions of the first mountain object s(r) against the scale r |
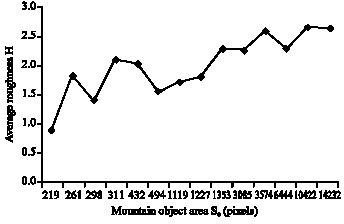 |
| Fig. 8: | Plot of the area of the mountains object S0 against the average roughness of the mountains object H |
The normalized probability functions of the mountain object s(r) are computed as the ratio of the area of pixels modified in the mountain object at each scale S(r) to the area of the mountain object S0.
(5) |
A larger value of s(r) indicates a larger area of convex and concave regions removed at scale r. As observed in Fig. 7, s(r) increases as the scale is increased, indicating the importance of multiscale analysis in surface roughness computation. At scales 19 and above, s(r) has a value of 0, indicating that all convex and concave regions in the mountain object have been removed.
The computed values of s(r) are used to compute average roughness of the extracted mountains H, which indicates surface roughness of the mountain object due to the convex and concave region distribution averaged over the area of the mountain object. H is computed using the following equation, which is due to Maragos (1989):
(6) |
H for the first mountain object is computed to be 1.79. The proposed procedure is employed to compute the values of H for the remaining mountains objects (Table 1). The proposed methodology allows for a more accurate quantification of a region’s convexity/concavity over varying scales, distinguishing between shallow and deep incisions and hence provides a more accurate surface roughness parameter. It is observed in Fig. 8 that the larger the area of the mountain object, the higher is its surface roughness. This observation is consistent with the findings reported in Miliaresis and Argialas (2002).
CONCLUSION
In this study, a procedure to compute the surface roughness of individual mountain objects extracted from Digital Elevation Models (DEMs) was proposed. First, mathematical morphology was employed to extract the mountains of the DEM. The lifting scheme was employed to perform the generation of multiscale DEMs. The mask of pixels modified in the each mountain object at each scale was computed by performing the intersection operation between the mountain object and the mask of pixels modified at each scale. The normalized probability functions for each mountain object were computed as the ratio of the area of pixels modified in the mountain object at each scale to the area of the mountain object. The computed normalized probability functions were used to compute the average size of convex and concave regions in the mountain objects and the scale-independent average roughness of the mountain objects due to the convex and concave region distribution averaged over the mountain objects. The proposed methodology allows for a more accurate quantification of a region’s convexity/concavity over varying scales, distinguishing between shallow and deep incisions and hence provides a more accurate surface roughness parameter. It was observed that the larger the area of the mountain object, the higher is its surface roughness.
ACKNOWLEDGMENTS
The author is grateful to four anonymous reviewers for their comments that have helped strengthen this study.