ABSTRACT
This study presents a new high-speed CMOS multiplier in nanotechnology. In this research, we have evaluated the effects of reduction technology size (from 130 to 80 nm) on power, delay and power-delay product of multipliers. Using nanotechnology scale electronic parameters had major effect in implementing multipliers in this research. We used HSPICE and Synopsys for simulations. A new multiplier, which accepts a redundant multiplicand, has been planned, simulated and compared with previous designs. A novel algorithm using carry save adder architecture and a new full - adder has been presented. To work at low power voltage, the pass transistor circuit that produces the XOR and XNOR outputs has been enhanced to solve delay problem. A carry-select adder has been implemented by using single ripple carry adder and an adder tree circuit. This research proposes a new adder tree using the high-speed circuits and multiplexers. Decreasing technology size with powerful design has decreased the power by 38% in these multipliers. The latency has decreased by almost 36% . Our design decreased transistor count by 32 %.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.2468.2473
URL: https://scialert.net/abstract/?doi=jas.2008.2468.2473
INTRODUCTION
With the advent of nanotechnology, the requirements for low power, high-speed design has become more important. Multipliers have an important effect on arithmetic processors performance. A new high-speed low-power multiplier has been presented in nanotechnology. Redundant number representation has been one of the essential aspects of computer arithmetic, which has been used in processor design to increase performance. The profits of using redundant number representations are obtained primarily from the ability to do carry-free addition. Unfortunately, in traditional processors the result of an operation must be changed back to traditional form before the instruction is completed. An improvement, which is possible for processors, is to use the result in redundant form, which avoids the delay related with conversion. The change to traditional form still must be done for saving stage, but this may be done in parallel with other operations. There has been interest in these techniques in which there is an additional pipeline stage added to the processor to hold the conversion step. The redundant form is done without passing through that pipeline step. Another purpose of this technique has been studied in Jou et al. (2003) which the redundant form is used in a multiply component.
Due to the fast growing mobile systems, not only faster arithmetic components but also smaller and low power arithmetic components are needed. However, it has been difficult to increase speed and reduction in area. In general, ripple adder provides a compressed design but suffers an extensive delay time. Carry lookahead adder gives a high-speed design but has a large area. Carry-select adder is middle of two other concerning in speed and area. Therefore, carry save adder is suitable in many applications that consider both speed and area. Carry save adder is also used with carry lookahead adder to increase the speed. This paper purposes a new structure to decrease area and power of carry save adder.
MATERIALS AND METHODS
This study started in 2007 at Islamic Azad University Varamin-Pishva branch. In the multiplication operation, P=X*Y, where X and Y are magnitudes in redundant representation and P is in traditional format as shown in Fig. 1. Block diagram of the multiply component has been shown.
It follows that Z = Y´*Xs + Y´*Xc where Y´ is Y recoded into radix 4, Y´ = (yn/2, yn/2-1,...,y0) for yi ε{-2, -1, 0, 2} for i < n/2, yn/2 ε{0,1,2} and Xs, Xc are the sum and carry bits of the carry save illustration.
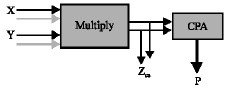 | |
| Fig. 1: | Block diagram of the multiply component producing redundant partial product Z and traditional partial product, P |
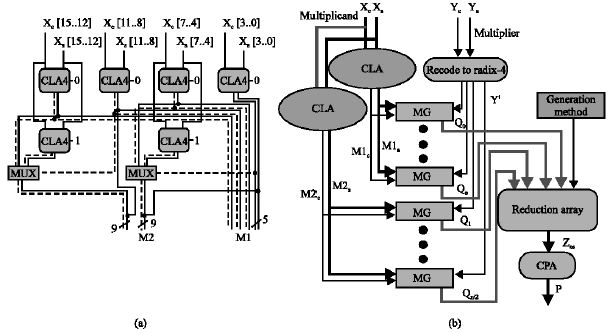 | |
| Fig. 2: | (a) An example of a carry lookahead adder which generates radix-2k1 and radix-2k2, k1 = 4, k2 = 8. Dashed lines show a single carry bit, solid lines are 4-bit. (b) A summation of the structure of the multiplier using carry lookahead adders to generate M1 and M2. The generator produces multiples, the indices e, f are chosen depending on the delay which can be tolerated in the reduction array |
In this case, this results to a multiplication by both Xs and Xc vectors. To reduce the size of the reduction array, the multiplicand is converted into radix-2k carry/save representation by slicing the multiplicand into k-digit groups. In this representation, the multiplicand is used which M = (ml-1,ml-2,...,m0) where mi ε{0,...,2k+1-1} and l = n/k for n digits. This can be split into two vectors, Ms and Mc, where Ms = Σmsi2i and ![]() and Msi, Mcj ε{0,1}. The value of k is essential, because as k increases, the delay of the conversion step increases while the amount of signals in the array decreases. There are at least two methods, which one can take to minimize the delay related with this conversion. The first way is to calculate the size of the group, k, across the multiplicand with the purpose of finding some mixture of group sizes, which minimizes the overall delay. The second way is to use different group sizes depending on which multiple outputs are used. The first way was studied widely, but did not make a delay as short as the second way, which is modified below for n = 32 and two grouping sizes, k1 and k2 = 8.
and Msi, Mcj ε{0,1}. The value of k is essential, because as k increases, the delay of the conversion step increases while the amount of signals in the array decreases. There are at least two methods, which one can take to minimize the delay related with this conversion. The first way is to calculate the size of the group, k, across the multiplicand with the purpose of finding some mixture of group sizes, which minimizes the overall delay. The second way is to use different group sizes depending on which multiple outputs are used. The first way was studied widely, but did not make a delay as short as the second way, which is modified below for n = 32 and two grouping sizes, k1 and k2 = 8.
Partial product reduction: The inputs to the array are the multiples, Qi in Fig. 2b. These inputs are reduced via a network of compressors. Some inputs to the array are used in the first step of the network (as in a traditional tree network), therefore, the delay of some Qi can be larger. An advantage of having a larger delay time for these Qi is that the value of k used for those multiples can be larger, with a equivalent reduction in the number of bits in Mc. To generate modified multiplicands with special values of k, a novel adder was proposed. The baselineology chosen is combination of the Carry Select adder and Carry Lookahead adder designs as shown in Fig. 2a. To reduce the hardware complexity of the conversion step, some of the outputs from the small groups are also used to produce the larger groups.
Multiple generations: The multiples, Qi ε{-2M, -1M, 0, 1M, 2M} for 0< i < n/2 and Qn/2 ε{0, 1M, 2M}, are produced from the recoded multiplier variable Y´ and multiplicand M. The multiples can be produced in a straightforward method given the multiplicand and the recoded multiplier bits where the output is a single bit variable. However, this method is not the wanted format when the multiplicand is in carry save adder form because there are two bits stream produced. These problems will be more difficult when producing negative multiples, since the empty positions in the carry stream become ones, which would affect the event of using sparse carry streams in the first place. To avoid this, a technique similar to that were proposed in Sunar and Koc (2001) is produced in which a constant, Bi, is added to the multiplicand to recompense for the ones produced by the multiples. The following example (Fig. 3) shows how this is done for n = 12, k = 4 and the multiplier in the {-2,-1,0,1,2}.
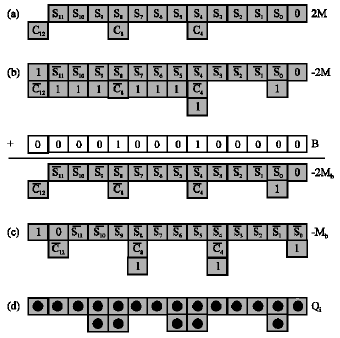 | |
| Fig. 3: | Generation method (a) The 2M multiple bits, (b) The -2M multiple bits with the ones arising after negating the carry stream. The constant, B, is also shown after addition step, the multiple, -2Mb is shown, (c) a procedure is followed to produce -Mb, using the same bias which results to an extra one in each carry column and (d) after adding the ones and using all multiples, the outputs Qi are shown |
Primary, the 2M multiple is presented with sum stream, S = Ms and carry stream C = Mc. Step (b) uses -2M with the ones produced by negating the multiple as in two`s complement form. The constant B is added to generate the multiple -2Mb with a carry stream, as in (a). Step (c) shows the consequence of adding the same constant to -M, but because of a shift in the position of the carry bit relative to B, not all ones are deleted. After adding the ones and computing with the other multiples, the outputs of Qi are shown in (d). The constant is calculated as:
(1) |
Which is a one just to the left of carry position, except the most significant, in Mc. The generator produces multiples, Qi as two bit streams, an n bit sum stream and a sparse carry stream. The carry stream has n/k groups of two bits divided by k two bit positions and an additional bit of value 2l for negative multiples. The last multiple does not use negative values, so the carry vector has only single bits divided by k-1 bit locations.
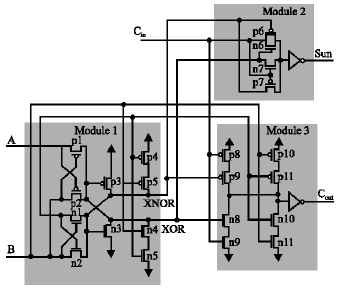 | |
| Fig. 4: | Three sub parts of the proposed novel full adder circuit |
To do correctness, there must be a recompense constant subtracted in the array, this constant, C is the sum of all Bi shifted suitably, ![]()
A novel high-speed adder: As shown in Fig. 4, the proposed full adder has three parts. The logic equations for the middle signals and outputs are given as follows:
(2) |
(3) |
(4) |
(5) |
One method to implement the XOR and XNOR gates is to synthesize the XOR gate and generate the XNOR gate through an inverter. This method of implementation has the difficulty of delaying one of the Y and Y´ outputs, giving rise to signal arrival time to the consecutive parts. This will enlarge the chance of generating fictitious switching and glitches in the last two parts. A better method is to use other sets of transistors to produce the XOR and XNOR gates individually, with the possibility of having a larger transistor count. To decrease the number of transistors, we use a pass transistor circuit with only six transistors to produce the balanced XOR and XNOR gates.
Compare with those designs that use an inverter to generate the complement signal, the switching speed is increased by deleting the inverter from the critical chain. The two complementary feedback transistors have the weak logic obtained by the pass transistors. They return the output by either pull it up through PMOS transistors to the power supply or pull it down through NMOS to ground so that enough drive is provided to the other parts. In addition, since there is no direct path between the Vdd and GND short circuit current has been decreased.
This circuit has the same voltage fall problem as other pass transistor circuits. The worst form delay happens at the state from 01 to 00 for AB. This could be realized with Fig. 4. When the circuit is at the transition of 01 for AB, logic 0 is going through the NMOS transistor and 1 goes through the PMOS transistor. However, when the next transition of 00 for AB obtains, a weak 0 (Vthp) is obtained through two PMOS pass transistors to the XOR output and XNOR is at high state. This 0 uses the feedback PMOS so that the XNOR output is pulled up to logic 1, which use the feedback NMOS to discharge the XOR output completely to ground. Thus, a voltage step happens at the output of XOR. Similar state happens at the conversion from 10 to 11 for AB, due to the lower Vthn and high electron transition of NMOS transistor, the entire procedure is faster than the previous case, which depends heavily on the PMOS switch. This slow response problem is more serious in low-voltage operation.
Due to the unacceptable performance at low-power voltage, we customized the circuit of Fig. 4. Two type PMOS transistors are used to resolve the worst-case delay problem of transition from 01 to 00 for AB. Two types NMOS transistors are used to resolve the problem of transition from 10 to 11 for AB. When the state of AB = 00 receives, the XNOR output could achieve a good 1 through two series PMOS pull-up transistors to the Vdd, which prevent the high state as in the previous example. Similarly, the XOR output could receive a strong 0 through two types NMOS pull-down transistors to ground when the state of AB changes to 11.
There are some methods for part 2. Since its logic equation is similar to that of part 1, the six transistor circuit can also be used. It suffers from inadequate driving power because of the pass transistors. In result of that, we use a related circuit, but fully make use of the presented XOR and XNOR outputs from module 1 to permit only a single inverter to be attached at the last step. The output inverter causes that adequate drive is obtained to the cascaded component. The least number of transistors for producing the Cout signal is two (circuit 10 transistor), but it has the threshold voltage drop problem. Although a four transistor circuit can be used to produce an appropriate Cout signal, it does not offer enough driving power. The presented circuit is based on CMOS logic method. Its logic equation is given by:
(6) |
This circuit has the benefits of complementary CMOS logic, which has been shown to be better in performance to all pass transistor logic for all logic function except XOR at high power supply. Its strength against voltage scaling and transistor sizing results to work consistently at low voltage and arbitrary transistor size. It has been a good experiment to treat the adder function as a stand alone component in simulation. It is also not usual that the adder functions that work well in such simulation still does not work upon actual implementation because of the weakness of driving power. This is because adder functions are normally chained to form a functional arithmetic circuit. Therefore, the adder functions must hold adequate drivability to provide the next component with appropriate inputs. The driving component must provide almost appropriate outputs to the driven components. Otherwise, the performance of the circuit will be decrease considerably or become unpractical at low power supply. For this reason, the adder components cannot be chained without buffers attached to the outputs of each module.
Proposed carry save adder architecture: Carry save adder is composed of many small ripple carry adder blocks. Thus, reducing the delay of ripple carry adders is important for designing a carry save adder. In order to optimize the ripple carry adder delay, all ripple carry adders in this paper use the mirror adders and the inverter elimination scheme in carry path (Kang and Gaudiot, 2006). The inverter elimination scheme uses two properties of the mirror adder. The first property is inverting all inputs on the full adder results in inverted values for all outputs. The second one is the mirror adder generates the complement of carryout first and inverts it to generate the carryout. Therefore, by putting even and odd cells as shown in Fig. 5, the number of the inverting stages in the carry path is reduced. This reduces n, x inverter delay in the carry pass where n is the block size. There is no transistor penalty for this scheme. In fact, one less transistor is used than the traditional full adder with 28 transistors.
A new adder tree circuit: Previous designs used half adders, inverters and multiplexers to perform the adder tree circuit, which is proposed as shown in Fig. 6. According to the previous complement method, a Sk1 is either the Sk0 or the complement of Sk0 where Sk0 shows a sum of kth bit for C = 0. Since the full adder produces both sum and the complement of sum, no extra inverter is needed to obtain the complement. To produce the adder circuit, a multiplexer is needed for each bit to select either Sk.
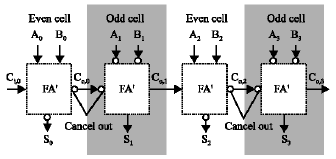 | |
| Fig. 5: | Inverter elimination in carry chain |
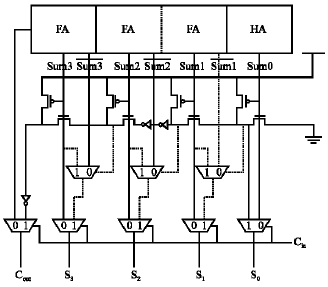 | |
| Fig. 6: | Proposed multiplexer-based adder tree circuit |
The control signal of the multiplexer achieves from the first circuit. The first circuit is NMOS and PMOS cascades as presented in the middle of Fig. 6. This circuit produces 0 at the kth node if no zero is produced until kth bit from the least significant bit; otherwise, it produces 1. If the control signal is 0, the multiplexer selects Sk; otherwise, it selects the inverted Sk. The least significant bit does not require a multiplexer since S01 is always the opposite value of S00. This needs a few transistors for each block. The carry out for a block can be selected between the carry out for the ripple carry adder or the carry out for the adder circuit is one if and only if all sums form the ripple carry adder are equal to one. When all sums are equivalent to one, the first circuit produces zero at the last node. For all other cases it produces one. Therefore, the inverted last node can be used as the carryout for C = 1. Finally, the multiplexers is suited in the bottom to select between the results for C = 0 and the results for C = 1.
The results present that proposed adder is faster than the traditional adder (Yeh and Jen, 2000; Cho et al., 2004). The worst-case delay happens when the carry chain form the LSB to MSB. In that case, the inputs for each adder are either (an = 1, bn = 1) or (an = 0, bn = 1) as well the LSB where both a0 and b0 should be 1.
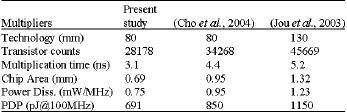
| Table 1: | Comparison between 54x54 bit multipliers |
 | |
The Cout for Cin =1 in a block generates and result a long delay time for Cout. Thus, if the arrival time of Cin is faster than the time for producing Cout for Cin = 1, the whole delay time become slower than the proposed adder where no carry chain occurred. The arrival times for the Cin and the Cout for Cin = 1 should be obtained to be the same. Then, the original carry save adder is faster than the proposed as predictable previously. However, it would be quite complicated since full adder delay is not equal to a multiplexer delay. Therefore, no carry propagation in the critical chain is preferred for a carry save adder design.
A multiplier core has been designed using 54x54 bits (Table 1). The multiplier is recoded in the standard method to radix-4 (Law and Rofail, 1999). The carry lookahead adder component has been selected with four bit carry network for the first two multiples and eight bit carry network for the remaining multiples. This results to an additional four bits in the largest column in the array. Since the simulation condition includes estimations of wire delay, buffers were stated in the multiplicand and the modified multiplier. The topology selected for buffer interconnects is one into two, with each of the two driving about half of the multiple producers.
It is understood, for the purposes of comparison, that whatever carry chain adder is used to change the result back to traditional form can be used for both the presented design and the traditional design. For this reason, the conversion component isn`t measured in this simulation and the traditional multiplier is planned in the same manner as above, with the exception that the carry lookahead adder is not shown. The buffer state is similar to that above.
Speedup: The delay profile information needs to be verified by calculating the speedup of the design. A program was designed to synthesize several standard programs by looking at functions of floating-point multiplication operands. The speedup, S, is determined only for floating-point multiply instructions and is calculated by,
(7) |
Where Trm is the delay the multiplier Tcm+Tc is the delay time of the traditional multiplier and f is the fraction of multiply operations, which could achieve its operand in redundant form. The time to do an exchange, Tc, is taken to be four nano-second, roughly one third of the time for a multiply operation. The latency has decreased by almost 36%.
CONCLUSIONS
A new multiplier for nanotechnology based systems has been designed and simulated. This study has presented a new high-speed low-power multiplier, which uses redundant operands. The design presented here can also easily be calculated to larger operands with a corresponding increase in performance, due to the logarithmic delay related with conversion to traditional form. Simulations have been done with HSPICE and Synopsys.
Replacing the ripple carry adder for C = 1 by the presented adder circuit with the complement method decreases the number of transistors of the carry save adder compared to the traditional and other carry save adders. The proposed adder required 38 and 29% fewer transistors, respectively. Fewer transistors show less area and less power. The power consumption of proposed carry save adder is calculated to be only 75% of the traditional carry save adders from the HSPICE simulation. The proposed 64 bit adder has 1.45 ns delay time at 2.5 V power supply using an 80 nm CMOS technology. Table 1 shows comparisons between multipliers. Decreasing technology size from 130 to 80 nm has decreased the power by 38% in these multipliers. The latency has decreased by almost 36%. Our design decreased transistor count by 32%.
REFERENCES
- Cho, K.J., K.C. Lee, J.G. Chung and K.K. Parhi, 2004. Design of low-error fixed-width modified booth multiplier. IEEE Trans. VLSI syst., 12: 522-531.
Direct Link - Jou, S.J., M.H. Tsai and Y.L. Tsao, 2003. Low-error reduced-width Booth multipliers for DSP applications. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 50: 1470-1474.
Direct Link - Kang, J.Y. and J.L. Gaudiot, 2006. A simple high-speed multiplier design. IEEE Trans. Comput., 55: 1253-1258.
Direct Link - Law, C.F., S.S. Rofail and K.S. Yeo, 1999. A low-power 16/spl times/16-b parallel multiplier utilizing pass-transistor logic. IEEE J. Solid State Circuits, 34: 1395-1399.
CrossRefDirect Link - Sunar, B. and C.K. Koc, 2001. An efficient optimal normal basis type II multiplier. IEEE Trans. Comput., 50: 83-87.
CrossRefDirect Link - Yeh, W.C. and C.W. Jen, 2000. High-speed booth encoded parallel multiplier design. IEEE Trans. Comput., 49: 692-701.
Direct Link








