Research Article
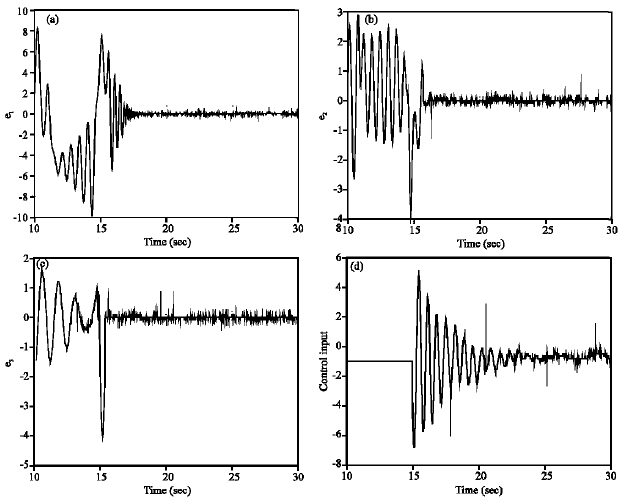
Design and Implement of a Digital PID Controller for a Chaos Synchronization System by Evolutionary Programming
Department of Electrical Engineering, Far-East University, No 49, Jung-Hwa Road, Hsin-Shih Town Tainan 744, Taiwan, Republic of China
Her Terng Yau
Department of Electrical Engineering, Far-East University, No 49, Jung-Hwa Road, Hsin-Shih Town Tainan 744, Taiwan, Republic of China
Yu Chi Pu
Department of Electrical Engineering, Far-East University, No 49, Jung-Hwa Road, Hsin-Shih Town Tainan 744, Taiwan, Republic of China












Abdulkarim Abubakar Reply
I appreciate with this, because it helps me in my project work litterature review, very interested and important
Editor
Thank you for your positive feedback. We are glad to hear that the research article on designing and implementing a digital PID controller for a chaos synchronization system has been helpful for your project work's literature review. We hope you find valuable insights and relevant information from the article to support your own research. If you have any further questions or need assistance, feel free to let us know.