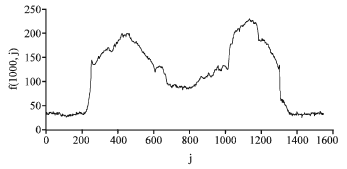
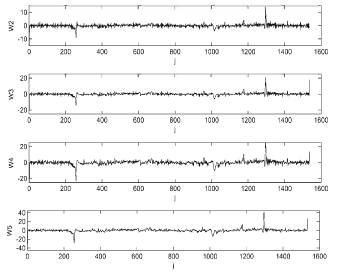
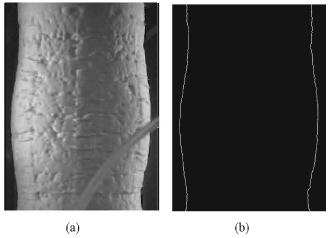
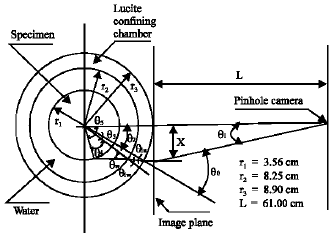
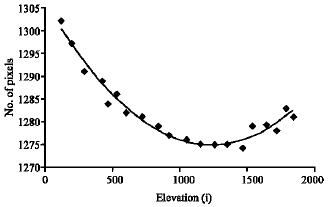
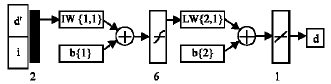
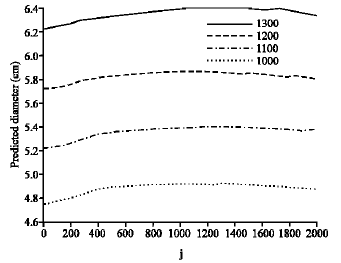
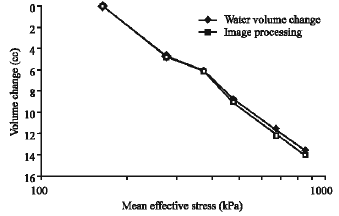
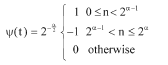Research Article
A Novel Approach to Measure the Volume Change of Triaxial Soil Samples Based on Image Processing
Department of Civil Engineering, School of Engineering, Shiraz University, Shiraz, Iran
G. Habibagahi
Department of Civil Engineering, School of Engineering, Shiraz University, Shiraz, Iran
A. Ghahramani
Department of Civil Engineering, School of Engineering, Shiraz University, Shiraz, Iran