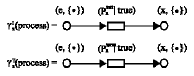
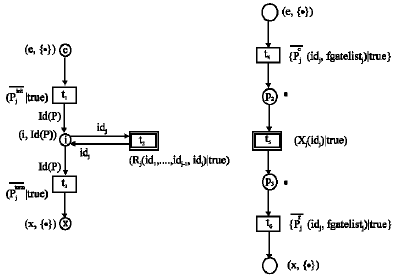
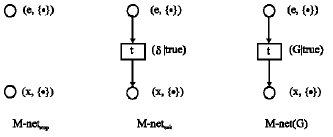
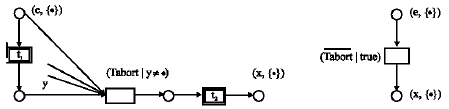
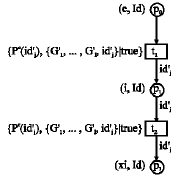
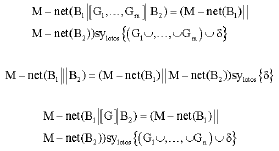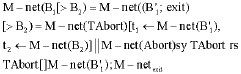Research Article
A Semantics for the Control Part of Lotos
Universite des Sciences et de la Technologie Mohamed Boudiaf, B.P. 1505, El Mnaouer, Oran, Algeria
B. Messabih
Universite des Sciences et de la Technologie Mohamed Boudiaf, B.P. 1505, El Mnaouer, Oran, Algeria