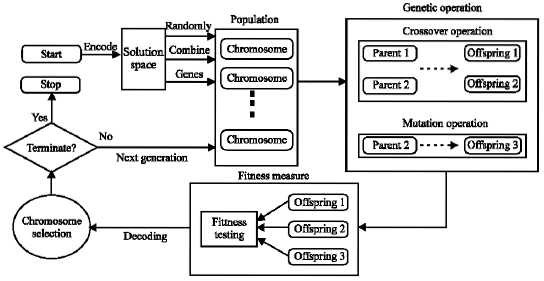
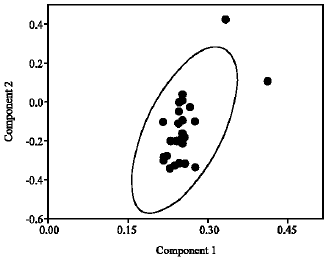
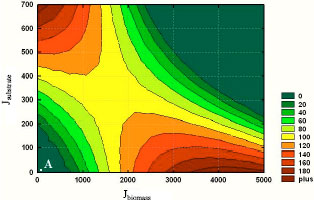
Research Article
Genetic Algorithms Using for a Batch Fermentation Process Identification
Groupe Modelisation de l`Information et des Processus, Laboratoire des Procedes Industriels, de Synthese et Environnement, Institut National Polytechnique Houphouet-Boigny, BP 1313 Yamoussoukro, Cote d`Ivoire
Assidjo N. Emmanuel
Groupe Modelisation de l`Information et des Processus, Laboratoire des Procedes Industriels, de Synthese et Environnement, Institut National Polytechnique Houphouet-Boigny, BP 1313 Yamoussoukro, Cote d`Ivoire
Akaki David
Groupe Modelisation de l`Information et des Processus, Laboratoire des Procedes Industriels, de Synthese et Environnement, Institut National Polytechnique Houphouet-Boigny, BP 1313 Yamoussoukro, Cote d`Ivoire
Yao K. Benjamin
Groupe Modelisation de l`Information et des Processus, Laboratoire des Procedes Industriels, de Synthese et Environnement, Institut National Polytechnique Houphouet-Boigny, BP 1313 Yamoussoukro, Cote d`Ivoire