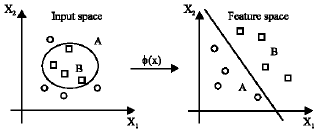
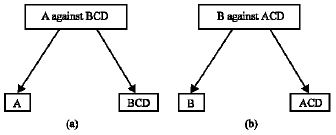
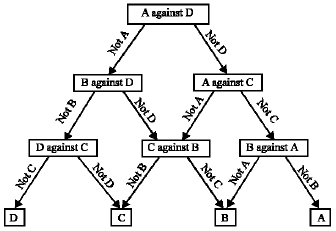
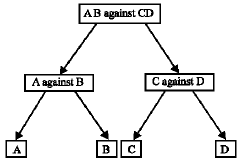
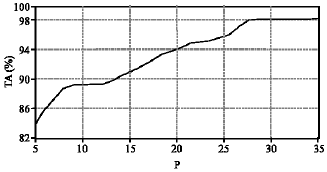
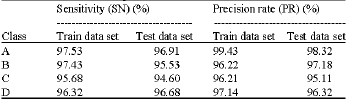
Research Article
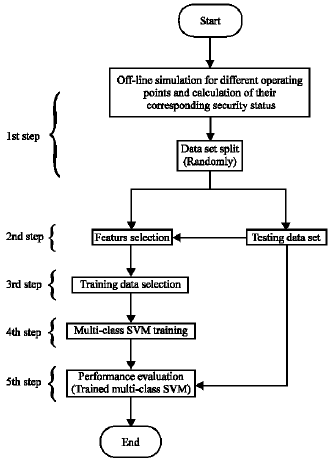
Power System On-Line Static Security Assessment by Using Multi-Class Support Vector Machines
No. 424, Hafez Ave, Department of Electrical Engineering, Amirkabir University of Technology, 15914, Tehran, Iran
G.B. Gharehpetian
No. 424, Hafez Ave, Department of Electrical Engineering, Amirkabir University of Technology, 15914, Tehran, Iran