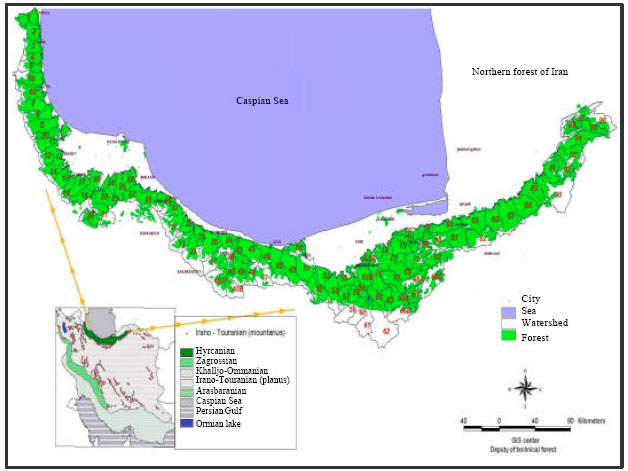
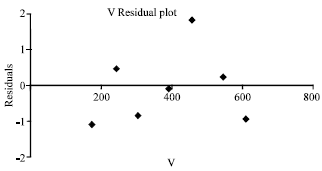
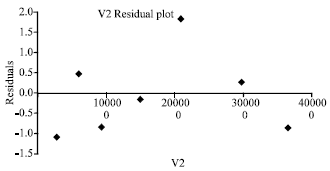
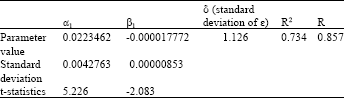
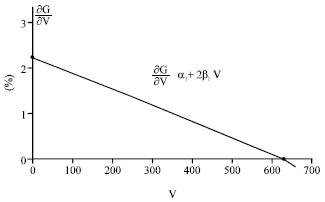
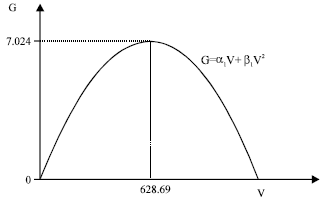
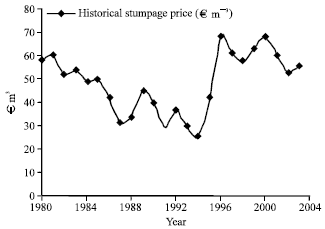
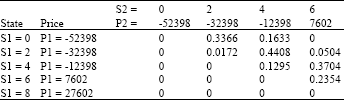
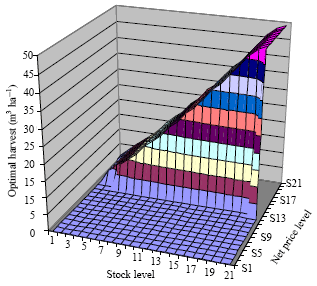
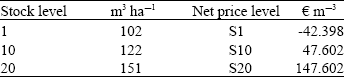
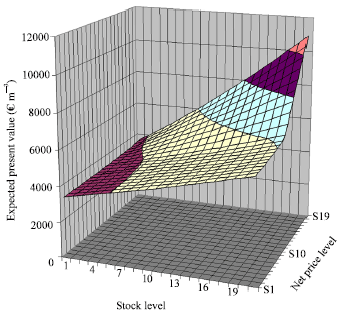
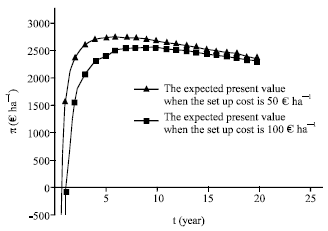
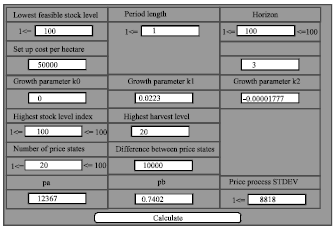
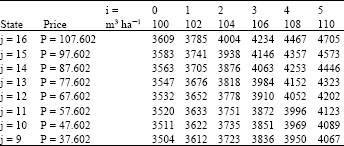
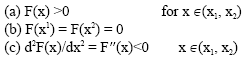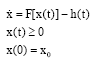Research Article
Optimal Continuous Cover Forest Management in an Uneven-Aged Forest in the North of Iran
Department of Forest Economics, Faculty of Forest Sciences, Swedish University of Agricultural Sciences (SLU), SE-901 83 Ume�, Sweden
S. Mohammadi Limaei
Department of Forest Economics, Faculty of Forest Sciences, Swedish University of Agricultural Sciences (SLU), SE-901 83 Ume�, Sweden