Research Article
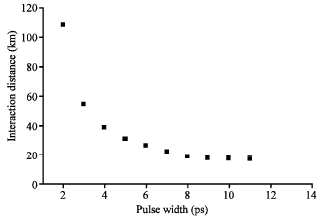
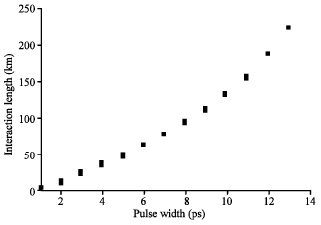
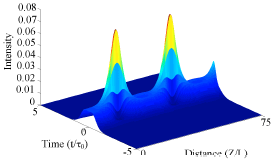
A Numerical Investigation of the Effects of Widths and Separation of Two Soliton Pulses on Their Interaction Distance
Department of Physics, University of Guilan, P.O. Box 1914, Rasht, Iran
S. Batebi
Department of Physics, University of Guilan, P.O. Box 1914, Rasht, Iran
H.R. Mashayekhi
Department of Physics, University of Guilan, P.O. Box 1914, Rasht, Iran