ABSTRACT
This study demonstrates a theoretical approach for capacitance matrix calculation of identical capacitances using the lattice Green`s function. The experimental results of equivalent capacitance between any two arbitrary points of a finite two dimensional capacitance network were in a good agreement with the calculated values.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.1987.1990
URL: https://scialert.net/abstract/?doi=jas.2008.1987.1990
INTRODUCTION
The calculation of capacitance between any arbitrary grid points in an infinite square matrix has a great practical and theoretical interest. Capacitance equivalent calculation represents an important electrical quantity in the design of multilayer dielectric medium systems and Very Large Scale Integration (VLSI) technologies (Gazizov, 2001, 2004; Yan and Trick, 1982; Ymeri et al., 2002). Recently, there have been a number of papers on the computation of capacitance matrix using on-surface MEI method, semi-analytical Green's function method and quasi-static analysis and Fourier series approach (Ymeri et al., 2002; Liu et al., 1999).
Lattice Green Function (LGF) play an important role in many physical calculations, such as the phase transition in classical two-dimensional lattice coulomb gases (Lee and Teitel, 1992), the interaction between the electrons which is mediated by the phonons (Rickayzen, 1980), the effect of impurities on the transport properties of metals (Economou, 1983), the transport in inhomogeneous conductors (Kirkpatrick, 1973) and the resistance calculation (Cserti, 2000; Cserti et al., 2002; Asad et al., 2006). Asad et al. (2006), Cserti (2000) and Cserti et al. (2002) studied the problem in which they used LGF to calculate the resistance between any two arbitrary points in a perfect and perturbed infinite square lattice.
In this study, the equivalent capacitance of a infinite square network was theoretically and experimentally obtained. The theoretical calculation of capacitance was based on the Green's Function method. The LGF presented in this research is related to the LGF of the Tight-Binding Hamiltonian (TBH) (Economou, 1983). Experimental results of equivalent capacitance between any two arbitrary points of a finite two-dimensional capacitance matrix (consisting of x identical capacitances) were measured using a digital LCR meter.
THEORETICAL CALCULATION
An infinite capacitance matrix consists of identical capacitances C, as shown in Fig. 1. The potential at lattice point r will be denoted by V(r). Then, we may write:
| (1) |
where, n are the vectors from point r to its nearest neighbors (n = ±ai, i = 1, ...,d). The right hand side of Eq. 1 may be expressed by the so-called lattice Laplacian defined on the hypercubic lattice (Cserti, 2000).
| (2) |
Thus Eq. 1, with the lattice Laplacian, can be rewritten as:
| (3) |
where the charge at lattice point r is:
| (4) |
The capacitance between the origin and ro is:
| (5) |
To find the capacitance we need to solve Eq. 3. This is a Poisson-like equation and may be solved by using the lattice Green's function:
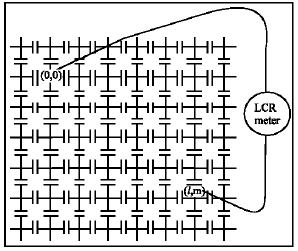 | |
| Fig. 1: | Infinite square capacitance network |
where the lattice Green's function is defined by Cserti (2000)
Using Eq. 4 and 5, the equivalent capacitance between the origin (0, 0) and the point (l, m) can be calculated by:
| (6) |
The capacitance between points (0, 0) and (1, 0) can easily be obtained as:
| (7) |
Lattice Green Function at the site (m, n) can be expressed from integral Green's function for square lattice with nearest neighbors interaction (Cserti et al., 2002; Asad et al., 2006):
| (8) |
where ε is the energy parameter.
By executing a partial integration with respect to x in Eq. 8, we obtained the following recurrence relation (Asad et al., 2006; Alzetta et al., 1994):
| (9) |
where G'(m,n) is the first derivative of G(m,n) with respect to ε.
Substituting (m,n) = (1,0), (1,1) and (2,0) in Eq. 9, respectively we obtained the following relations
| (10) |
| (11) |
| (12) |
For m = 0 we obtain:
 | (13) |
For m ≠ 0 we have:
 | (14) |
Insert n = 0 in Eq. 13 we find the relation (where G(1,0) = G(0,1) = G(0,-1) due to the symmetry of the lattice, δ0,0 = 1 and ε = 1):
| (15) |
Thus, Eq. 7 becomes
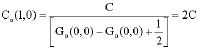 | (16) |
To calculate the capacitance between the origin and the second nearest neighbors (i.e., (1,1)) then:
| (17) |
Substituting (m, n) = (1,0), (1,1) and (2,0) in Eq. 14, respectively we obtained the following relations
| (18) |
| (19) |
| (20) |
Using the symmetry of lattice and substituting Eq. 15 we obtained the following relations:
| (21) |
| (22) |
| (23) |
Now, by taking the derivative of Eq. 23 with respect to ε and using Eq. 10-12, we obtained the following expressions:
| (24) |
(25) |
| (26) |
| (27) |
Again, taking the derivative of both side of Eq. 24 with respect to ε and using Eq. 10 and 15, we obtained the following differential equation for G(0,0):
| (28) |
By using the following transformations ![]() and x = ε2 we obtain the following differential equation (Ashcroft and Mermin, 1976; Kittel, 1986)
and x = ε2 we obtain the following differential equation (Ashcroft and Mermin, 1976; Kittel, 1986)
This is called the hypergeometric differential equation (Gauss's differentia equation). So, the solution of the differential equation is Y(x) = (2/π)K(ε), then:
| (29) |
By using Eq. 29 we can express G'(0,0) and G"(0,0) in terms of the complete elliptic integrals of the first and second kind K(ε) and E(ε) are the complete elliptic integrals of the first and second kind, respectively.
| (30) |
| (31) |
So that, the two dimensional LGF at an arbitrary site is obtained in closed form, which contains a sum of the complete elliptic integrals of the first and second kind.
Go(1,1) can be expressed in terms of Go(0,0) and G'(0,0) as:
| (32) |
Where:
| (33) |
Substituting the last two expressions into Eq. 17, one obtains:
| (34) |
Finally, to find the capacitance between the origin and any lattice site (l, m) one can use the above method. Here there are some calculated values
Co(2,0) = 1.3761C, Co(3,0) = 1.16198C and Co(4,0) = 1.0483C
EXPERIMENTAL RESULTS
To study the capacitance of a finite square lattice experimentally we constructed a finite square network of identical (25x25) capacitances, each have a value of 2.2 μF. Using the constructed network, the capacitance between the origin and the site is measured using a digital LCR meter SE8280.
The calculated and measured capacitance along the (10) and (11) directions are shown in Fig. 2 and 3, respectively.
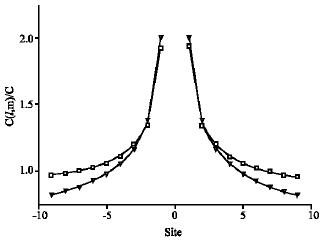 | |
| Fig. 2: | The capacitance of a square lattice; calculated (Δ) and measured (□) along the (01) direction |
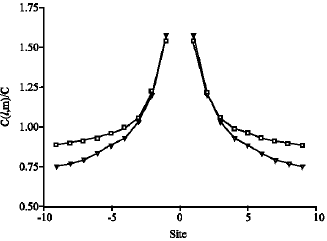 | |
| Fig. 3: | The capacitance of a square lattice; calculated (Δ) and measured (□) along the (11) direction |
From Fig. 2 and 3, it can be noticed that curves of a measured values along the directions (10) and (11) are symmetric. Also, show that the theoretically calculated values are closed to the experimentally measured values.
CONCLUSIONS
This study demonstrates a theoretical approach for calculating the capacitance between two arbitrary lattice points in an infinite square lattice using a Tight-Binding Hamiltonian (TBH) Lattice Green Function (LGF). Experimental results obtained for a finite square network consisting of 25x25 identical capacitances are in a good agreement with the theoretically calculated values. Data show that the calculated and measured values along the (10) and (11) directions are symmetric under the transformation (l,m) → (—l,—m) due to the inversion symmetry of the lattice.
REFERENCES
- Alzetta, G., E. Arimondo, R.M. Celli and F. Fuso, 1994. Simple method for resistance measurements on thin films and bulk of high Tc superconducting materials. J. Phys. III France, 4: 1495-1501.
CrossRefDirect Link - Asad, J.H., A. Sakaji, R.S. Hijjawi and J.M. Khalifeh, 2006. On the resistance of an infinite square network of identical resistors-theoretical and experimental comparison. Eur. Phys. J. B, 52: 365-370.
CrossRefDirect Link - Cserti, J., 2000. Application of the lattice Green's function for calculating the resistance of an infinite network of resistors. Am. J. Phys., 68: 896-904.
CrossRefDirect Link - Cserti, J., D. Gyula and P. Attila, 2002. Perturbation of infinite networks of resistors. Am. J. Phys., 70: 153-163.
CrossRefDirect Link - Gazizov, T.R., 2001. Analytic expressions for MOM calculation of capacitance matrix of two dimensional system of conductors and dielectrics having arbitrarily oriented boundaries. IEEE Int. Symp., 1: 151-155.
Direct Link - Gazizov, T.R., 2004. Calculation of a capacitance matrix for a two-dimensional configuration of conductors and dielectrics with orthogonal boundaries. Russian Phys. J., 47: 326-328.
Direct Link - Lee, J. and S. Teitel, 1992. Phase transitions in classical two-dimensional lattice Coulomb gases. Phys. Rev. B, 46: 3247-3262.
CrossRefDirect Link - Liu, W.Y., K. Lan and K.K. Mei, 1999. Computation of capacitance matrix for integrated circuit interconnects using on-surface MEI method. IEEE Microwave Guided Wave Lett., 9: 303-304.
CrossRefDirect Link - Yan, C.P. and T.N. Trick, 1982. A simple formula for the estimation of the capacitance of two-dimensional interconnects in VLSI circuits. IEEE Electron Device Lett., 3: 391-393.
CrossRefDirect Link - Ymeri, H., B. Nauwelaers and K. Maex, 2002. Efficient procedure for capacitance matrix calculation of multilayer VLSI interconnects using quasi-static analysis and Fourier series approach. J. Telecommun. Inform. Technol., 3: 40-44.
Direct Link








