Research Article
An Investigation of Code Matched Interleaver for 3G Turbo Code Systems
Multimedia University, 63100, Cyberjaya, Selangor, Malaysia
S. Kalpana
Multimedia University, 63100, Cyberjaya, Selangor, Malaysia
Turbo codes have attracted attention since introduced in 1993 (Berrrou et al., 1993). Turbo codes are a parallel concatenation of two or more convolutional codes separated by pseudo random interleaver, therefore the characteristic of both constituent encoder as well as the interleaver is important in order to achieve good performance. In turbo code system, properly designed interleavers could enhance the BER performances.
Both existing 3G communication standards-WCDMA and cdma2000-adopting turbo codes as a component for error control coding in respective standards (ETSI, 2000; 3GPP2, 2002). Basically, 3G interleavers are based on ROM (Read Only Memory) and RAM (Random Access Memory) where ROM based interleaver depends on the pre-generated patterns by random address generation software while RAM based interleaver calculate the addresses and store the value in it. The interleavers used in both systems are complex and need a long mathematical computation process (Ramasamy and Siddiqi, 2006). Code Matched Interleaver (CMI) was introduced in Feng et al. (2002) which combines both pseudo-random interleaver and S-random interleaver that either eliminate low weight code words or reduce the number of low weight code words that could not be eliminated.
In this research, we presented an investigation on the performance of turbo code system in both 3G systems using Code Matched Interleaver (CMI) as the internal interleaver in the turbo encoder.
TURBO CODE SYSTEM
In typical turbo code system, a turbo encoder consists of two identical constituent Recursive Systematic Convolutional (RSC) encoders with an interleaver preceding the second constituent encoder as shown in Fig. 1. Turbo decoding principle is shown in Fig. 2. Basically, the performance of a turbo code system may be affected by different parameters of the component codes, block sizes, interleaver design and weight spectrum.
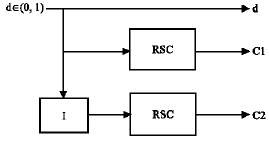 | |
| Fig. 1: | Turbo encoder |
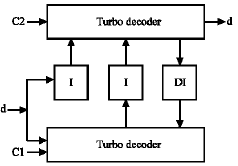 | |
| Fig. 2: | Turbo decoder |
The interleaver has a key role in shaping the weight distribution of the code, which ultimately controls the BER performance of the system.
Turbo code in WCDMA system: WCDMA is an evolution of GSM and uses a broader spectrum and the signaling is based on GSM system. WCDMA standard (3GPP TS 25.2123G) allows a range of frame size from 40 to 5114 bits with code rates 1/3 and 1/2. WCDMA turbo encoder uses 8 states identical RSC encoders with an internal interleaver (ETSI, 2000). The internal interleaver consists of bits-input to a rectangular matrix with padding, intra-row and inter-row permutations of the rectangular matrix and bits-output from the rectangular matrix with pruning. The generator polynomial used in the system is (13/11) and Log-MAP algorithm used in decoding process.
Turbo code in cdma2000 system: cdma2000 turbo encoder consists of a pair of rate 1/3 system atic convolutional encoders with constraint length, K = 4 separated by an interleaver (3GPP2, 2002). The interleaver consists of block interleaver, frame quality indicator and reserved bits input. The cdma2000 system uses RSC encoder with generator polynomial [(13:15)/11]. The frame size of this system (as well as the interleaver) must be one of the following specific values: 378, 570, 762, 1146, 1530, 2398, 3066, 4602, 6138, 9210, 12282 or 20730 bits with code rates from 1/2, 1/3 and 1/4. Log-MAP used as the decoding algorithm.
PROPOSED CODE MATCHED INTERLEAVER DESIGN
A good interleaver design for a turbo code is the one produces high weight output (Andresen and Zylabov, 1997; Divsalar and Pollara, 1995). The proposed Code Matched Interleaver (CMI) could substitute the existing 3G internal interleavers. CMI interleaver is divided into two parts: (1) S-random interleaver and (2) Pseudo random interleaver. The principle behind the S-random interlever is to spread the position of the elements within a window as far as possible, such that any two elements within a window size of S will not locate in a window of size S at the same time. The idea underlying in pseudo random interleaver design is to remove some apparent order such that low weight parity output sequences would not occur on both upper and lower constituent encoder at the same time. The design of the CMI interleaver can be formulated as follows (Feng et al., 2002):
| • | Eliminate low weight code words with significant contributions to the error performance. |
| • | Reduce the number of other low weight code words, which could not be eliminated. |
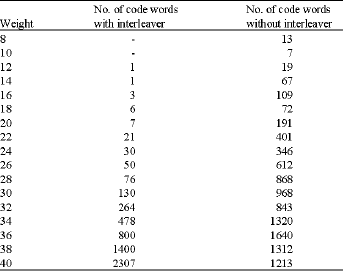
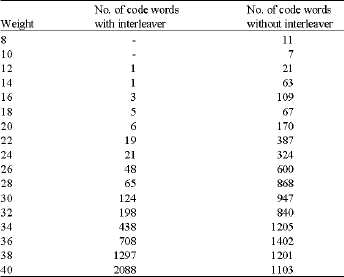
The elimination of a specific code word can be done by breaking up the input pattern that generates that specific code word. An interleaver with S-random constrain can either break short weight-3 input sequences with lengths up to S+1 or expand it to a longer one with lengths more than 2(S+1), where ![]() (Feng et al., 2002). Therefore, we consider breaking weight-2 and weight-4 input patterns in our interleaver design. The complete weight spectra for several short block length proposed turbo codes are obtained. The algorithm for computing the turbo code free distance is based on the 3G turbo sub codes, i.e., a subset of a code defined via constraints on the edges of its trellis and permits the computation of large distances for large interleavers without a constraint on the input sequence weight. The weight spectrum of the both 3G systems with N = 400 (WCDMA) and N = 378 (cdma2000), code rate = 1/3 shown in Table 1 and 2.
(Feng et al., 2002). Therefore, we consider breaking weight-2 and weight-4 input patterns in our interleaver design. The complete weight spectra for several short block length proposed turbo codes are obtained. The algorithm for computing the turbo code free distance is based on the 3G turbo sub codes, i.e., a subset of a code defined via constraints on the edges of its trellis and permits the computation of large distances for large interleavers without a constraint on the input sequence weight. The weight spectrum of the both 3G systems with N = 400 (WCDMA) and N = 378 (cdma2000), code rate = 1/3 shown in Table 1 and 2.
From Table 1 and 2, we identified the code words that should be broken are those with weight 12, 14, 16, 18 and 20. It was identified that the code words with weights 12 and 16 are generated by input patterns with weights 3, 4, 5, 6, 7, 8, 9 for WCDMA and 3, 4, 5, 6, 7 for cdma2000. The code with weights 14, 18 and 20 are generated by input patterns with weight 2, 3, 4, 5, 6, 7, 8 for WCDMA and 2, 3, 4, 5, 6 and 9 for cdma2000.
For both 3G systems, the weight-2 input patterns which produces lowest weight parity check sequence c2 is x2 = (00…010000100…), where the distance between two 1’ is μ = 5. The parity check c2 = (00…011001100…), where zmin = 4.
| Table 1: | The weight spectrum of WCDMA system with and without interleaver |
 | |
| Table 2: | The weight spectrum of cdma2000 system with and without interleaver |
 | |
If the interleaver maps the input weight-2 sequence with μ to a sequence with the same weight and μ, the resulting overall codeword weight is:
| (1) |
A weight-2 input sequence that generates a finite weight parity check sequence can be represented by Divsalar and Pollara (1995):
| (2) |
where, k1 = 1, 2, 3…Y and τ1 is the time delay. The parity check weight of Eq. 2 is given by:
| (3) |
If the interleaver maps (2) to X’2 (D) = (1+Dμk2)Dτ2, the overall weight of the generated codeword is given by:
| (4) |
where, y1 and y2 are the first and second encoder output, respectively. Then the overall weight of the codeword generated by weight-2 input sequence is:
| (5) |
We consider breaking the input patterns that generate code words with weight no longer than 20 only. Then we have
| (6) |
which equivalent to
| (7) |
Let j1 and j2 be the positions of 1’ in the weight-2 input sequence, where j1, j2∈A and α(j1) and α(j2) ∈A. The following mapping conditions should be satisfied to avoid mapping the input sequence to another weight-2 input sequence that generates a finite code word length:
| (8) |
where, μ is the minimum distance between two 1’ in the weight-2 input pattern that generates the finite weight code word. We can consider weight-4 input sequences as the compound of two single weight-2 sequences:
| (9) |
The input to the second encoder,
X’4 (D) = (1+Dμk’3)Dτ3 + (1+Dμk’4)Dτ4
where, t2 > t1 + μk’1, t4 > t3 + μk’1. The overall weight of the generated code word can be calculated from Eq. 4 is:
d = 4 + y1(4) + y2(4)/(zmin — 2) = 12 + (k’1+k’2+k’3+k’4),
which is equivalent
| (10) |
Let j1, j2, j3 and j4 be the positions of 1’ in the weight-4 input sequence, where j1, j2, j3 and j4 ∈ A and j1 < j2 < j3 < j4. Let α(j1), α(j2), α(j3) and α(j4) be the positions of 1’ in the interleaved input sequence α(j1), α(j2), α(j3) and α(j4) ∈ A. The following mapping conditions should be satisfied to avoid mapping the input sequence that includes two weight-2 input patterns, which generates finite code word length:
| α(j1) - α(j3) | mod μ ≠ 0 and | α(j2) - α(j4) | mod μ ≠ 0 whenever | (j1) - (j2) | mod μ = 0 and | (j3) - (j4) | mod μ = 0 or,
| α(j1) - α(j4) | mod μ ≠ 0 and | α(j2) - α(j3) | mod μ ≠ 0 whenever | (j1) - (j2) | mod μ = 0 and | (j3) - (j4) | mod μ = 0.
However in both cases of weight-2 and weight-4 input patterns, only those input patterns that generate low-weight code words with large contributions to the performance needs to be broken. So for both cases, we consider the input pattern that generate code words with weight no larger than 20 only. The effect of input patterns with weight greater than 4 on code performance is small and they can be typically broken by the S-random constraint. The algorithm used (Yuan et al., 1999) for the interleaver design is described as follows:
| • | Generate an integer randomly from the set (1, 2, 3, ….. N) where N is the interleaver size. The selected integer represents the position of the interleaver. |
| • | Each randomly selected integer is compared to the S previous selected integers. If the absolute value of the difference between the current selected integer and any of the S previous selected integers is smaller than S, then reject the current selected integer and go to step 1. |
| • | Check whether the current interleaver output satisfies the mapping conditions given in Eq. 7, 8, 10 and 11-If not go to step 1. |
| • | If no integer from the set can satisfy both steps 2 and 3 simultaneously, for a large number of iterations, then reduce S by 1 and start the search again. |
| • | Save the current integer. The process is repeated until all N integers are selected. |
| • | Exit |
SIMULATION RESULTS
To verify the suitability of CMI for both 3G standards, we simulate the performance of both 3G turbo code systems using 3G Interleavers and proposed CMI. For WCDMA system, simulations were carried out for information block length, N = 5114, code rate 1/3 using Log-MAP decoder with maximum decoding iteration is 8 and 14 over AWGN and uncorrelated Rayleigh fading channel. In cdma2000 system, simulations were carried out for the information block length, N = 6138, code rate 1/3 using Log-MAP decoder with maximum decoding iterations is 9 for AWGN channel and 12 for uncorrelated Rayleigh fading channels. Fading amplitude α = 1 for AWGN channel and 0.8662 for Rayleigh channel. Both simulation results are shown in Fig. 3 and 4.
From Fig. 3, it is observed that the system with proposed CMI, performs better than the system with 3G interleaver in both cases with coding gain about 0.2-0.35 dB In Fig. 4, it is found that the system with proposed CMI, performs better than the system with 3G interleaver in both cases with coding gain about 0.15-0.3 dB.
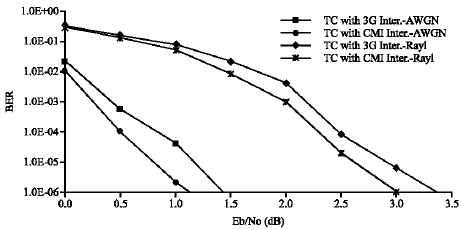 | |
| Fig. 3: | Simulation results for WCDMA system |
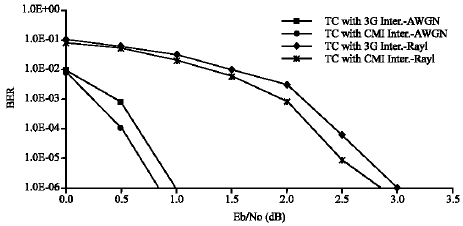 | |
| Fig. 4: | Simulation results for cdma2000 system |
We have investigated the usage of Code Matched Interleaver in 3G turbo code system, which suits both 3G Communication standards-WCDMA and cdma2000. The Code Matched Interleaver studied through a meticulous finding on the weight spectra of both 3G turbo code systems. The simulation results indicate the performance of 3G turbo code system with CMI performs better than turbo code system with 3G interleavers. The coding gain of the system is from 0.15-0.35 dB for different channel conditions.