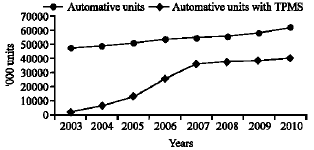
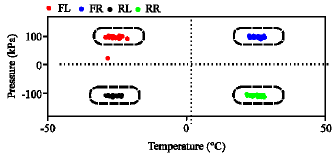
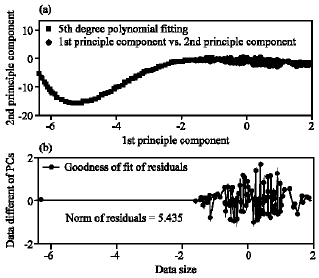
Research Article
TPMS Data Analysis for Enhancing Intelligent Vehicle Performance
Signal Processing Research Group, Department of Electrical, Electronics and Systems, Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor DE, Malaysia
A. Hussain
Signal Processing Research Group, Department of Electrical, Electronics and Systems, Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor DE, Malaysia
A. Mohamed
Signal Processing Research Group, Department of Electrical, Electronics and Systems, Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor DE, Malaysia
S.A. Samad
Signal Processing Research Group, Department of Electrical, Electronics and Systems, Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor DE, Malaysia