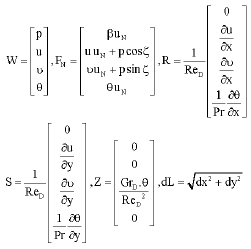
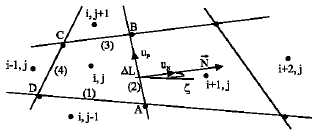
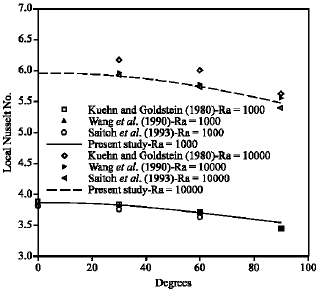
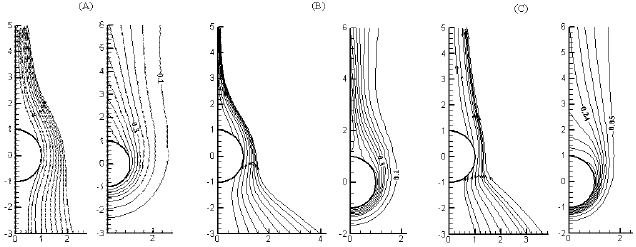
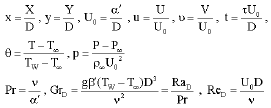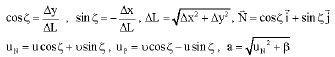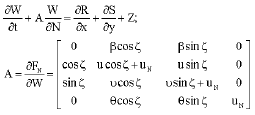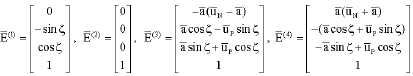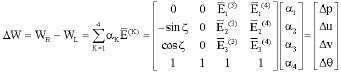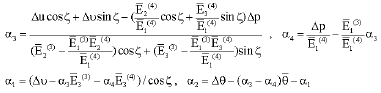Research Article
Characteristics-Based Finite-Volume Solution for Natural Convection Around a Horizontal Cylinder
Faculty of Mechanical Engineering, University of Tabriz, Tabriz, Iran
Farzad Barar
Faculty of Mechanical Engineering, University of Tabriz, Tabriz, Iran
Vahid Farhangmehr
Faculty of Mechanical Engineering, University of Tabriz, Tabriz, Iran