Research Article
Decision Criteria for Optimum Machining Control
Department of Information Management, Yu Da College of Business, Miaoli County, Taiwan 361, Republic of China
Cutting conditions for a cutting tool have been the most critical variables in machining process. Cutting speed, feed rate and depth of cut were considered as three factors of input cutting parameters (Montgomery, 1976). Koren et al. (1991) have described several methods to be used under stepwise constant variation in feed, speed, or depth of cut, but none is practically applicable when two or more cutting conditions are changed. Hence, the method of controlling cutting conditions with fixed material removal rate has been introduced (Balazinski and Ennajimi, 1984; Davim and Antonio, 2001). For most studies with this viewpoint, the material removal rate is fixed because of the expensive observation of control. However, through the computer-integrated interface to program the machining feed rate on modern Computer Numerical Controlled (CNC) machines with fixed cutting speed and depth of cut, the material removal rate is capable of being dynamically controlled (Yeh and Lan, 2003).
In addition, Choudhury and Appa Rao (1999) described that tool life is the critical parameter of the cutting process. Novak and Wilklund (1996) proposed a suitable implementation to predict tool life and Lee et al. (1992) proposed a method of optimal control to ensure maximum tool life. As a matter of fact, maximal tool life will not guarantee the maximum profit of machining. Besides, the various tool checking periods for a tool change from different machine tool operators will decrease the productivity and increase the cost during the machining significantly. In order to well manage the consumption of tools, a fixed tool life is practically considered for the cutting process in this study.
Moreover, the cost to machine each part is a function of the machining time (Jung and Ahluwalia, 1995). From Kamien and Schwartz (1991), the marginal cost of production is a linear function of production rate (Lan et al., 2002, 2008). Therefore, the marginal cost of operation is also proposed to be a linear function of the material removal rate in this study. This explains that more machining rate causes more operational cost such as machine maintenance, loading-unloading and machine depreciation costs.
According to Galante et al. (1998), the dependency of a reliability model on the cutting conditions is the aim to optimize the manufacturing system. Although several time series modeling on the control of machining process are mentioned for decision-making (Kim et al., 1996), none is capable to achieve the maximum profit. They are all emphasizing on the maximum tool usage or minimum tool cost. Practically, the profit and the productivity of a machining process are the mostly concerned problems confronting the manufacturing industry. Besides, the need of operating CNC machines efficiently to obtain the required payback is even greater in the case of rough machining, since a greater amount of material is removed thus increasing possible savings (Meng et al., 2000). With the reasons above, there is an economic need to control the material removal rate of rough machining operation for a cutting tool. Hence, the need of controlling the material removal rate with fixed tool life to achieve the maximal profit for a cutting tool is absolutely arising.
Nevertheless, the traditional machining model (fixed machining rate model) may surpass the DMC model under certain conditions. Thus, the demand to compare two models is also appeared. Therefore, the decision criteria for selecting the optimal machining model are then desired in this field.
ASSUMPTIONS AND NOTATIONS
Assumptions
| • | The cutting process is a continuous rough turning operation with one type of tool. |
| • | Each tool performs the same fixed length of cutting time (tool life). |
| • | The upper speed limit of material removal rate is generated from the maximal machining conditions (speed, feed rate and depth of cut) suggested in the machining handbook and the fixed tool life is obtained from the Taylor’ tool life equation (DeGarmo et al., 1997) with these selected conditions. Thus, no tool will break before this fixed tool life even with the upper speed limit. |
| • | There is no chattering or scrapping of parts occurs during the machining process. |
| • | All chip from cutting and finished parts are held in the machine until a tool change. |
| • | All parts are moved to other department and paid at a given price immediately after machining operation at the tool change. |
Parameters and Notations
| A | : | Fixed MRR of the traditional machining model |
| a | : | Average volume of material removed per unit part machined. |
| B | : | Upper speed limit of material removal rate. |
| bMR′(t) | : | Marginal operation cost, including all labor and machine costs, at the material removal rate MR′(t); where b is a constant. |
| bMR′ 2(t) | : | Operational cost at time t. |
| c | : | Overall holding cost per unit chip per unit time, where c = h1 + h2/a. |
| h1 | : | Chip holding cost per unit chip per unit time. |
| h2 | : | Part holding cost per unit finished part per unit time. |
| P | : | Contribution per unit part machined. |
| [0,T] | : | Controlling time interval of tool life. |
Decision functions
| MR(t) | : | Cumulated volume of material removed during time interval [0,t]. |
| MR′(t) | : | Material removal rate at time t. |
THEORETICAL BACKGROUND
In the previous research (Yeh and Lan, 2002), the cutting process is regarded as a continuous single-tool turning operation without breakdown. That is, the machine is operated within the tool life and it will not break even with the highest machining rate from the handbook. The data for both the fixed tool life time and the upper MRR limit are obtained from the maximal machining conditions suggested in the machining handbook. In general, if the machine is operated within the tool life time, it will not break even with the highest machining rate.
In this study, ![]() means the contribution of one tool under machining operation with a fixed tool life T. Whilst Kamien and Schwartz (1991) described the marginal operation cost of production is a linear increasing function of production rate and the operational cost is directly proportional to the square of the production rate, the operational cost of a machine is also proposed in direct proportion to the square of the material removal rate in this study. Thus,
means the contribution of one tool under machining operation with a fixed tool life T. Whilst Kamien and Schwartz (1991) described the marginal operation cost of production is a linear increasing function of production rate and the operational cost is directly proportional to the square of the production rate, the operational cost of a machine is also proposed in direct proportion to the square of the material removal rate in this study. Thus, ![]() represents the operational cost during time interval [o,T].
represents the operational cost during time interval [o,T].
|
denote the chip holding cost and finished part holding cost during time interval [0, T], respectively. Therefore, the objective function for maximum profit of each tool is described as:
Set c = h1 + h2/a be the overall holding cost per unit chip per unit time. Thus, the DMC model is developed as:
 |
Set MR′*(t) and MR*(t) be the optimal solution of DMC model and assume that time interval ![]() is the maximal subinterval of [0,T] to satisfy Euler Equation (Kamien and Schwartz, 1991; Chiang, 1992).
is the maximal subinterval of [0,T] to satisfy Euler Equation (Kamien and Schwartz, 1991; Chiang, 1992).
There are two feasible situations to be discussed. They are proposed as follows.
Situation 1: MR*′(t) will not touch B before T. ![]()
In this case, it is assumed that MR′(t) will never reach the upper speed limit B before tool life time T. From Euler Equation (Kamien and Schwartz, 1991; Chiang, 1992), the transversality condition of salvage value for free MR(t) (Kamien and Schwartz, 1991; Chiang, 1992) and the boundary conditions, one can obtain the optimal solution (Yeh and Lan, 2002) for Situation 1 as:
| (1) |
| (2) |
Before finding the optimal solution for Situation 2, one Property is proposed by Yeh and Lan (2002) as follows:
Property: If the line y = MR*′(t) touches the line y = B, these two lines should overlap to be y = B from the touch point ![]() to the end point T.
to the end point T.
Proof: From Eq. 1, the optimal control of MR*′(t) is a strictly increasing linear function of t. And it holds for the subinterval of [0,T] subject to 0 ≤ MR*′(t) ≤B. Since the straight line in the time interval ![]() cannot exist because it contradicts Euler Equation (Kamien and Schwartz, 1991; Chiang, 1992) to be a decreasing linear function of t, the property is verified.
cannot exist because it contradicts Euler Equation (Kamien and Schwartz, 1991; Chiang, 1992) to be a decreasing linear function of t, the property is verified.
Situation 2: MR*′(t) will touch B before T. ![]()
In this case, we assume that MR′(t) will reach the upper limit B at time ![]() . From the transversality condition of salvage value for free end value MR(
. From the transversality condition of salvage value for free end value MR(![]() ) (Kamien and Schwartz, 1991; Chiang, 1992) and the Property, one will have
) (Kamien and Schwartz, 1991; Chiang, 1992) and the Property, one will have
| (3) |
Therefore, the optimal solution (Yeh and Lan, 2002) for Situation 2 is shown as follows:
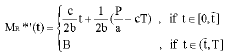 | (4) |
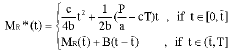 | (5) |
COMPARISON OF TRADITIONAL AND DMC MODEL
After the dynamic solution of machining control is achieved, the comparison to the traditional model with fixed material removal rate A (fixed speed, feed rate and depth of cut) is then necessarily taken. Here, both models are assumed to receive positive profits. Thus, the two feasible cases are then discussed as follows.
Case 1: The optimal control of MRR does not touch the upper speed limit B.
Whenthe DMC model is the optimal solution for the control of material removal rate.
Whenthe traditional machining control model may be the optimal solution. For
the traditional model is optimal, where
The detailed process is developed in Appendix A.
Case 2: The optimal control of MRR touches the upper speed limit B.
Whenthe DMC model is the optimal solution for the control of material removal rate.
Whenthe traditional machining control model may be the optimal solution. For
the traditional model is optimal,
where |
The detail is developed in Appendix B.
DECISION CRITERIA
With Eq. 3, there are two situations to be considered. They are described as follows.
Situation 3: If , ![]() will not touch B before
will not touch B before ![]()
From the discussion of comparing two machining models, the decision criteria to select the optimal machining model for Situation 3 is then proposed and described as follows.
Whenthe DMC, Dynamic Machining Control, Model is optimal.
Whenthere are three possible conditions.
Forthe traditional machining control model is optimal.
Forthe DMC model is optimal.
Forwithin [0,B], both the DMC and traditional models are optimal.
Situation 4: If , ![]() will touch B before T.
will touch B before T. ![]() .
.
From the discussion of comparing two machining models, the decision criteria to select the optimal machining model for Situation 4 is also proposed and described as follows.
Whenthe DMC model is optimal.
Whenthere are three possible conditions.
Forthe traditional machining control model is optimal.
Forthe DMC model is optimal.
Forwithin [0,B], both the DMC and traditional models are optimal.
The tool life, operational cost, holding costs, contribution per unit part machined, average volume of material removed per unit part machined and upper speed limit are considered simultaneously to dynamically optimize the control of material removal rate. It is an extremely hard-solving and complicated issue. However, with the DMC model, the problem becomes concrete and solvable.
In addition, four characteristics of the optimal solution for DMC model are illustrated as follows: First, the optimal material removal rate MR*′(t) is a strictly increasing linear function of t before reaching the upper limit. Second, by Property, if the optimal material removal rate MR*′(t) touches the upper speed limit B, it will stay to be B for the rest of the tool life. Third, by Eq. 3, the overall holding cost per unit chip must be smaller than the contribution per unit material removed. Otherwise, the optimal material removal rate may reach zero. Fourth, with Eq. 4, two times of the marginal cost at upper speed limit must be larger than the contribution per unit material removed. Otherwise, the optimal material removal rate may reach the upper speed limit.
Moreover, the comparison of DMC model and traditional model to approach the decision criteria is fully discussed. And the typical conditions for traditional model to surpass DMC model are also presented. In Situation 3, when ![]() and
and
the traditional model is optimal. Furthermore, with the comparison of two models, the decision criteria for selecting the optimal control of material removal rate are then suggested.
This study not only provides the idea of automatic control on material removal rate to machine tool manufacturer, but also leads the cutting process toward to reach maximum profit. Future researches on the modeling of dynamic optimization on multi-tool machining processes and the production project control with deadline constraint are surely encouraged. In sum, this study definitely generates an adaptable concept of machining control to the technology and contributes a better and practical tool for decision-making to this field.
Appendix A
Substituting Eq. 1 and 2 into the objective of DMC model, it is derived that
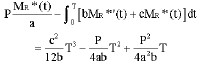 | (A1) |
In addition, the objective of the traditional machining control is described and rearranged as below.
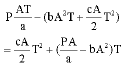 | (A2) |
With Eq. A1 subtracting Eq. A2, the difference between the objectives of two models is then found as:
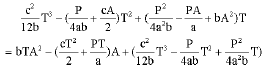 |
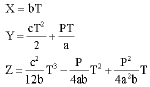 |
Also, set the difference of two models as a function y(A). Hence, the function is written as:
| (A3) |
It is observable that X, Y >0. And, from Eq. (A1), it is also known that Z>0
From Eq. (A3), we then have
| (A4) |
| (A5) |
By Eq. A5, it is noticed that y′′(A)>0. This denotes that the curve function of A is concave.
The minimum value of curve function y(A) occurs when y′(A) = 0. From Eq. A4, we have
Therefore, the minimal value of the curve function y(A) is shown as:
| (A6) |
From Eq. A6 and A3, the criteria are then derived.
Appendix B
Substituting Eq. 4 and 5 into the objective of DMC model, it is then modified as:
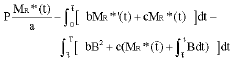 |
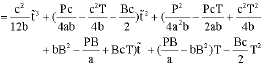 | (B1) |
With Eq. B1 subtracting Eq. A2, the difference between the objectives of two models is then obtained as:
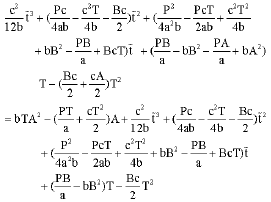 |
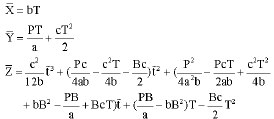 |
Also, set the difference of two models as a function ȳ(A). Hence, the function is written as:
| (B2) |
It is observable that x̄ ȳ >0. And, from Eq. B1, it is known that ![]() .
.
From Eq. B2, we then have
| (B3) |
| (B4) |
Again, by Eq. B4, we know that ![]() . This denotes that the curve function
. This denotes that the curve function ![]() is also concave.
is also concave.
The minimum value of curve function ![]() occurs when
occurs when ![]() . From Eq. B3, it is obtained that
. From Eq. B3, it is obtained that
Therefore, the minimal value of the curve function ![]() is found as:
is found as:
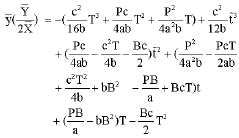 | (B5) |
Substituting Eq. 5 into Eq. B5, it is derived that
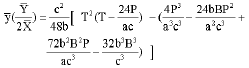 | (B6) |