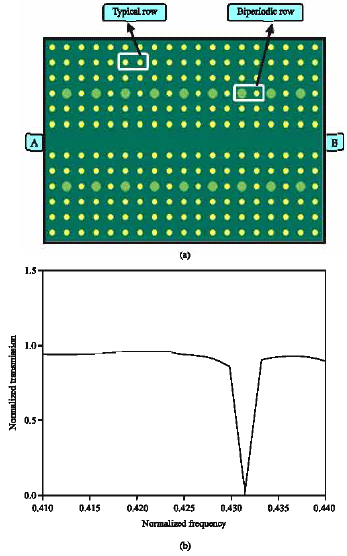
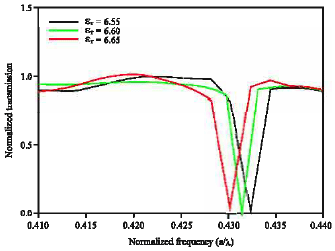
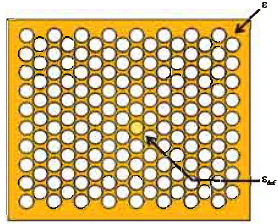
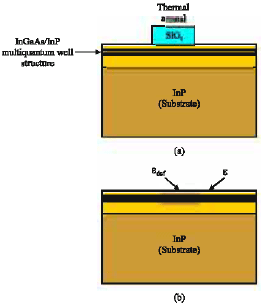
Research Article
Photonic Crystal Narrow Band Filters Using Biperiodic Structures
Department of Electrical Engineering, K.N. Toosi University of Technology, Tehran, Iran
A. Ghaffari
Department of Electrical Engineering, K.N. Toosi University of Technology, Tehran, Iran
F. Monifi
Department of Electrical Engineering, K.N. Toosi University of Technology, Tehran, Iran
M.S. Abrishamian
Department of Electrical Engineering, K.N. Toosi University of Technology, Tehran, Iran