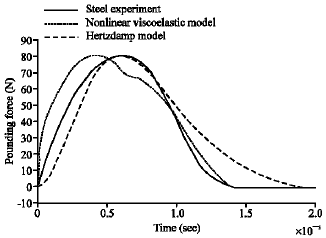
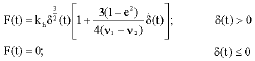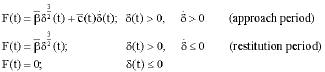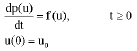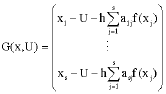Research Article
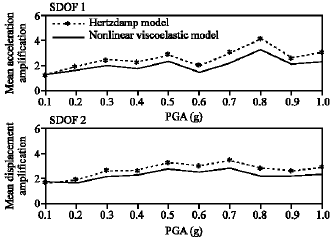
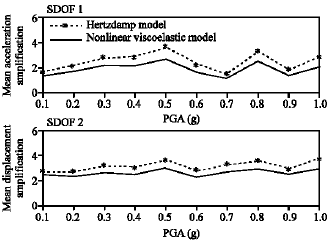
Structural Pounding Models with Hertz Spring and Nonlinear Damper
1Department of Mathematical Sciences, Faculty of Science and Technology, Hirosaki University, Hirosaki 036-1861, Japan
Xiaojun Chen
2Department of Applied Mathematics, Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, China
Robert Jankowski
3Faculty of Civil and Environmental Engineering, Gdansk University of Technology, ul. Narutowicza 11/12, 80-952 Gdansk, Poland