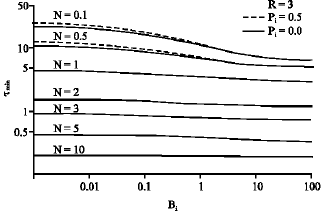
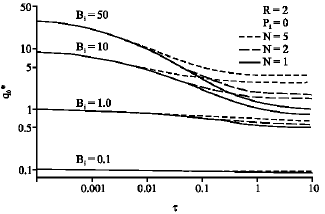
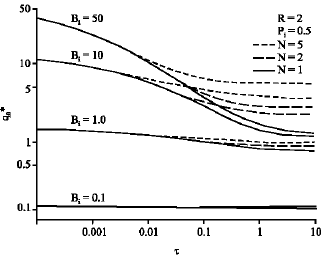
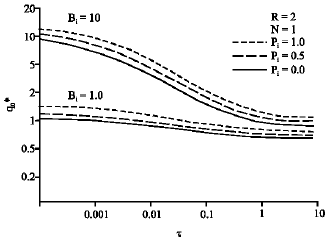
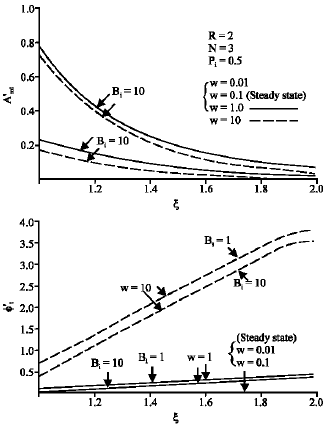
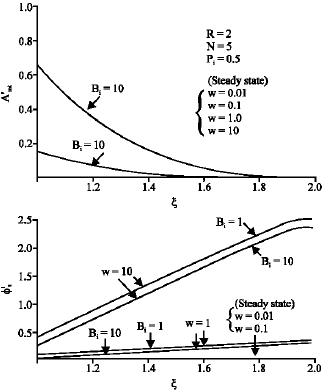
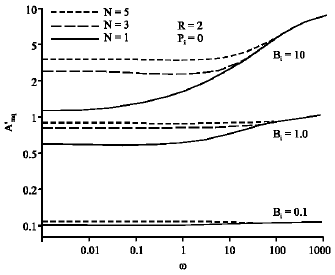
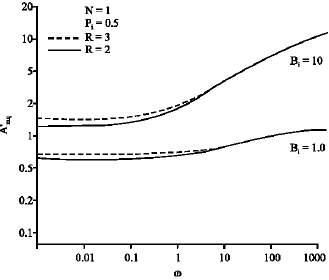
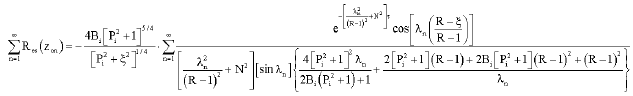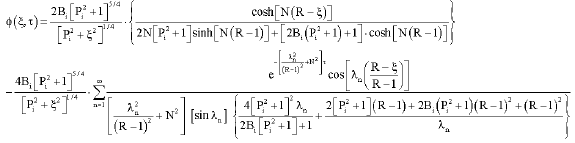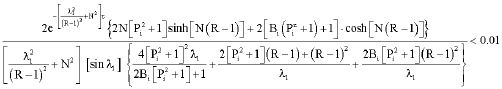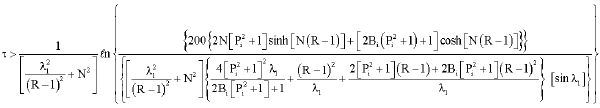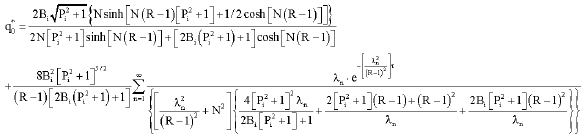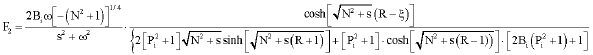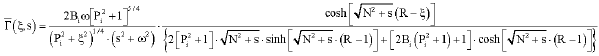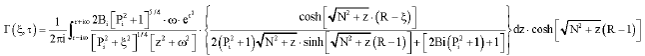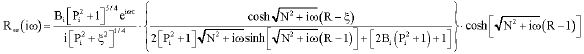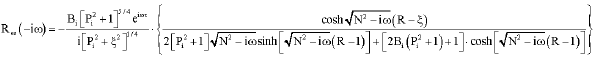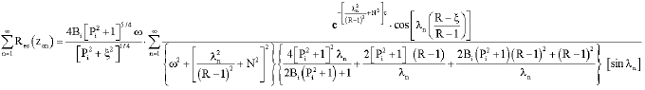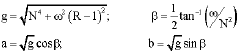Research Article
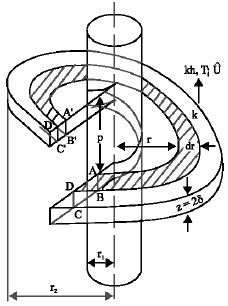
Transient Response of a Spiral Fin with its Base Subjected to the Variation of Heat Flux
1Department of Power Mechanical Engineering, National Taitung College, Taitung, Taiwan
W.J. Luo
2Department of Refrigeration, Air-Conditioning and Energy Engineering, National Chin-Yi University of Technology, Taiping City, Taichung County 411, Taiwan
S.P. Hsu
2Department of Refrigeration, Air-Conditioning and Energy Engineering, National Chin-Yi University of Technology, Taiping City, Taichung County 411, Taiwan