ABSTRACT
In this study, a novel serial concatenated coding scheme (Block Turbo Codes-BTC)-Forward Error Correction (FEC) codes-to mitigate error in high speed (>10 GHz) fiber optic communication is proposed and analyzed through simulation results. With combination of Reed Solomon and Reed Muller component codes-RS (255,223)+RM(1,5) outperform ITU-T G.975 RS (255.239) FEC recommendation with coding gain 1.95-2.00 dB.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.1796.1797
URL: https://scialert.net/abstract/?doi=jas.2008.1796.1797
INTRODUCTION
For high-speed broadband networks, the data transmission reliability provided by the network may be lower than the reliability requested by an application. In this case, the transport protocol of the network must compensate for the differences in the bit loss rate. The main basic scheme for improving the reliability is Forward Error Correction (FEC). FEC is widely used in wired and mobile communication, deep space communication as well as data storage systems (Roman, 1992). In the recent years, it has begun to find application in optical networks. In optical communication systems that operates at high data rate, it is challenge to find low overhead codes that capable of correcting random errors due to noise and burst errors due to dispersion and inter-channel cross talk with special emphasis on complexity and cost. Basically, the FEC is divided into two types of codes- convolutional codes and block codes. It is difficult to adopt convolutional codec in fiber optic system because the code rate (Rc) required for the system is Rc>0.8 (Agrawal, 1997). Therefore, block codes, which capable of correcting multiple bit errors with low overhead constrain preferred. Algebra block codes such as BCH (Bose-Chauduri-Hocqueaghem), RS (Reed-Soloman) and RM (Reed-Muller) are the popular codes. As transmission speed increases on one hand, the transmission impairments also increase on the other. In many cases, the impairments increase in nonlinear fashion, even though the transmission rate is increasing linearly. Hence, we need a powerful FEC to overcome this problem in both single-channel and multi-channel WDM system for delivering error free transmission (Sab and Lemaire, 2000). According to ITU.T G.975 recommendation, RS (255,239) code has error correction capability but it is not sufficient as we looking forward for data transmission which is higher than 10 G bit/s. Hence, we have proposed serial concatenated coding scheme which combines RS codes and RM codes as outer and inner codes respectively. The concatenated based block code is called Block Turbo Codes (BTC).
ENCODING AND DECODING SYSTEM
The overall encoding and decoding scheme shown in Fig. 1. The RS outer code is interleaved with DxN interleaver. The encoding is accomplished in two stages- outer and inner, where at second stage of encoding, the array stored in interleaver is encoded in the RM codes and the code is decoded with iterative Turbo decoding scheme.
At the first stage of encoding, for the outer RS codes, we have selected two candidate codes-RS (255.223) and RS (255.239) ITU.T G.975. The performance of each of these codes in proposed BTC will be evaluated through simulation. Then, the encoded codeword stored in an interleaver. Each column of array consists of one byte of RS codeword. After that, each column of the array in the interleaver is encoded in the RM (1.5) code which is (32.6) RM inner code of Hamming distance 16 (Dumer and Krichchevskiy, 2000). The codewords transmitted using BPSK modulation scheme. Then, it goes through the Additive White Gaussian Noise (AWGN) channel. At the decoder, it consists of two stages, the inner and outer decoding. Inner decoding is done first followed by the outer decoding. The maximum number of iterations is 3.
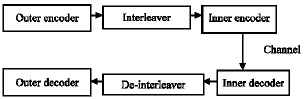 | |
| Fig. 1: | BTC scheme |
SIMULATION RESULTS AND DISCUSSION
The simulation for the system was done using Monte Carlo simulation. The system considered in this study is high speed optical transmission system (≥10 Gb/s/channel).
The results are shown in Fig. 2 for BTC–[RS (255.223)+RM(1.5)] and [ RS (255.239)+ RM (1.5)]. At the same time, the proposed BTCs are compared with typical ITU scheme- RS (255.239) and other BTC such as RS (255.239)2, RS (255.223)2.
It can be shown from Fig. 2, the proposed BTC outperform other codes, where the BTC RS (255.223)+ RM (1.5) codes is better than the BTC RS (255.239)+ RM (1.5) with coding gain nearly 0.49-0.51 dB.
The performance result of the BTC [RS (255.223) and RM (1.5)] is attractive and gave better coding gain compare to other FEC codes due to as follows:
| • | Both RS and RM codes are capable of correcting multiple bit error with low overhead constrains |
| • | The outer code RS has the capability of a powerful error correction block code with high code rate; its has large number of Hamming distance (d) with large error correcting capability (t) (Wu et al., 1994). As for comparison of RS (255.223) and RS (255.239); The minimum Hamming distance for RS(255.223) is 33 and RS (255.239) is 17. Therefore, the correcting capability of RS (255.223) is much more higher than RS (255.239). Moreover, the code rate = n/k, for RS (255.223) is 0.8745 while RS(255,239) is 0.9372. Since, the code rate of RS (255.223) is smaller than RS (255.239), thus, the performance value of RS (255.223) is better than RS (255.239). |
| • | Meanwhile, the inner code rate RM (1.5) which has length of n = 2m and code distance, d = 2m-r. For the decoding algorithm for inner code of this proposed BTC, for the fixed order–r; it has error correcting capabilities of weight up to (d*ln d)/4. Therefore, for RM (1.5) of our proposed BTC, the system could correct most of the error patterns of weight up to 11, which contribute in enhancement of the BER performance through better correction ability. |
| • | Overall combination of RS (255.223) and RM (1.5) code as outer code and inner code, respectively, could give better error mitigation properties. |
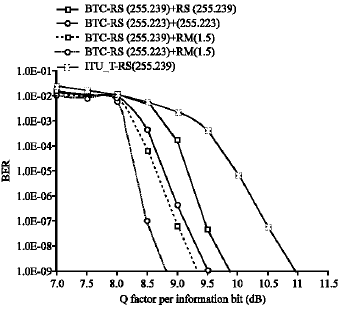 | |
| Fig. 2: | Simulated performance results for BTC [RS (255.239)+RM(1.5)]; [RS(255.223)+RM (1.5)]; RS (255.239)2; RS (255.223)2 and ITU_T RS (255.239) |
CONCLUSION
We have compared the performance of proposed BTC codes with the other codes including the typical FEC used in fiber optic communication. It was clear that the proposed BTC RS (255.223)+RM (1.5) has better performance value which means good error correction capability and applicable for high data transmission for more than 10 G bit/s. Hence, the proposed code could be used as FEC in higher speed fiber optic network.
REFERENCES
- Dumer, I. and R. Krichchevskiy, 2000. Soft Decision Majority Decoding of RM Codes. IEEE Trans. Inform. Theor., 46: 258-264.
Direct Link - Sab, O.A. and V. Lemaire, 2000. Block turbo codes performance for long haul DWDM optical transmission systems. Opt. Fiber Conf., 3: 280-282.
Direct Link - Wu, J., S. Lin, T. Kasami, W. Fujiwara and T. Takata, 1994. An upper bound on the effective error co-efficient of two-stage decoding and good two-level decomposition of some RM codes. IEEE Trans. Commun., 42: 813-818.
CrossRefDirect Link








