ABSTRACT
The basis of Positron Emission Tomography (PET) is the detection of the photons produced, when a positron annihilates with an electron. Conservation of energy and momentum then require that two 511 keV gamma rays are emitted almost back to back (180° apart). This method is used to determine the spatial distribution of a positron emitting fluid. Verifying the position of a single emitting particle in an object instead of determining the distribution of a positron emitting fluid is the basis of another technique, which has been named positron emitting particle tracking PEPT and has been developed in Birmingham University. Birmingham University has recently obtained the PET scanner from Hammersmith Hospital which was installed there in 1987. This scanner consists of 32 detector buckets, each includes 128 bismuth germanate detection elements, which are configured in 8 rings. This scanner has been rebuilt in a flexible geometry and will be used for PEPT studies. Testing the PEPT algorithm on ECAT scanner gives a high data rate, can track approximately accurate at high speed and also has the possibility of making measurements on large vessels.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.1738.1743
URL: https://scialert.net/abstract/?doi=jas.2008.1738.1743
INTRODUCTION
PEPT is a technique for studying the motion of a positron labelled particle within a closed, circulating system (Parker et al., 1993). The basis of PEPT is detecting coincidently a pair of opposite annihilation photons. Detecting both photons defines a line and the annihilation is assumed to have occurred somewhere along this line. By detecting of a number of annihilation events in 3D and using triangulation, the tracer location can be determined.
The application of PEPT to industrial process systems carried at the University of Birmingham is categorized in two subjects: the behaviour of granular materials and viscous fluids. Granular materials are processed in industry for example in the manufacture of pharmaceuticals, ceramics, food and polymers (Parker et al., 1994). PEPT allows the possibility of tracking a single particle within the fluidised bed also for studying systems such as: fluid flow, viscous fluids in mixers (Parker et al., 1995).
In PEPT, a single tracer particle is introduced into the system and can be tracked as it moves. When two gamma rays are detected at particular point in space may be positron annihilation occurred somewhere along the line joining these points which is called trajectory (Fig. 1).
In emission detection all events (coincidence, scatter and random) can be detected. If there are only two coincidence events, with using triangulation the location of the single positron emitter can be localized.
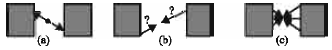 | |
| Fig. 1: | Principle of tracer particle, (a) Coincident detection, (b) possible location of point source and (c) Reconstruction of detection |
In other words, in the absence of scatter and random events all paths for reconstruction will be passed close to a single positron emitter. But in the case of presence of random and scatter events a signification fraction of the reconstructed gamma ray paths will not pass close to the tracer position. So corrupt events (random and scatter) have to discarded to get an accurate location of the tracer in PEPT. The process of the PEPT algorithm will be described as follows.
Suppose that (x, y, z) are the coordinates of the point which is closest to all of the reconstruction paths (their gamma rays path). With using an analytical process those paths which are furthest from closest point will be discarded as corrupt. This process will be repeated for the remaining paths. The algorithm will be iterated until a fraction f of the original events remain. The fraction f depend on some factors such as:
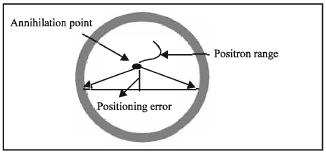 | |
| Fig. 2: | The effect of positron range, positioning error and detector separation |
| • | The electron and positron are not completely at rest when they annihilate. So the effect of this unstationary is the two gammas will be emitted at not exactly back to back. This results in a small positioning error, which depend on the detectors separation. |
| • | The amount of scattering material presents in the system. If the material in the system cause more scatter events then, process of calculation of closes point takes more time and the inaccuracy goes up. |
| • | Positron range which is defined as the distance that the positron travels before it annihilates (Fig. 2). |
The accuracy of location in PEPT is described below as: Suppose there is a slow moving tracer (or stationary tracer) and its location can consider within the value ?. If N be the number of coincident events then standard deviation of N measurement is σ. Since there are corrupt events (random and scattered) so the precision of location of tracer in N measurement is given approximately by:
| (1) |
where, N` = f N is the number of gamma ray paths used in the final calculation after corrupt events have been discarded and f is fraction of original events which is remaining (Parker et al., 1994). The focus of this research is on the testing the PEPT algorithm on a ECAT Scanner at the Birmingham University.
ECAT scanner: Since 1999, PEPT studies at Birmingham University have used an ADAC Forte positron camera consisting of two large sodium iodide detectors (Parker et al., 2002).
In 2002 the Positron Imaging Center acquired a medical PET scanner (Fig. 3a) an ECAT 931/08, previously at Hammersmith Hospital. This scanner has 4096 Bi4Ge3O13 (BGO) crystals which are arranged in 8 rings (Fig. 3b). Bismuth germanate scintillation material has high density. When it is combined with a photomultiplier it provides high photopeak efficiency for the detection of 511 keV gamma rays and in the ECAT scanner the detection rate is up to 2 million coincidence events/second. Each individual crystal has dimensions of 12.9 mm axial, 5.6 mm transaxial and 30 mm thickness giving an efficiency of over 50%.
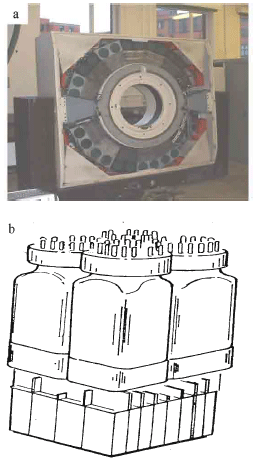 | |
| Fig. 3: | (a) A photo of the ECAT scanner without couch and with covers removed, b) Components of BGO detector (4x8 matrix of BGO), light guide and 4 photomultipliers |
The crystals are grouped in detector block units (4x8 crystals each) viewed by four photomultipliers. This scanner consists of 32 detector buckets. Each bucket comprises 4 detector blocks so that in total the scanner consists of 8 rings each of 512 elements. The detectors are housed in a gantry arranged in rings with 102 cm internal diameter giving a 65 cm transaxial field of view (FOV) and 10 cm axial FOV. Fifteen planes are imaged over the 10 cm axial field of view. To maximize the cross sectional imaging of no axially oriented objects under investigation the gantry can tilt up to ±90° from the horizontal axis and rotate ±45° about a vertical axis.
This scanner has two extremely valuable advantages for PEPT. The first is that, since the bismuth germanate has high density so we expect to have high sensitivity for detecting gamma rays. This means it will provide high count rates and hence more precise tracking of a tracer. Second its modular construction makes it possible to change its geometry into a more flexible geometry in order to do PEPT tests on larger systems.
Modification of ECAT scanner for list mode: In normal operation, detected events were immediately binned into arrays representing the total number of gamma rays detected at each position and angle over the duration of the scan.
For PEPT, we need the data to be recorded in list mode. This means that the details of every event were individually recorded on disk with the time at which the event occurred. We have modified the software controlling data acquisition, so as to record data in list mode with time stamps every 1 m sec.
First PEPT test on ECAT scanner at original configuration: Initial tests used the scanner in its original geometry, with the buckets mounted in two rings. For some reason only one complete ring of buckets was assembled and tested.
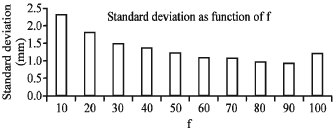
The simplest test of the precision of the positron emission particle tracking technique was to locate a stationary particle nearly in the center of the detector and determine its position. The point source was placed in centre of the detector. Coincidence data were recorded in buffers which was operator selectable. Then a PEPT algorithm estimate of the axial and transaxial position of the tracer particle. The data were recorded to list mode and was analysed with using a variety of different parameters in the tracking algorithm. Then mean value of these locations was calculated and the standard deviations of the locations σx, σy, σz about this mean value in each of the three coordinates were calculated. After that 3D standard deviation was obtained. Figure 4 shows the variation of standard deviation σ = (σ2x+σ2y+σ2z) versus f.
As it is clear there is an optimum point for f and it is around 85%. Too small value of f makes calculation worse. This part of diagram completely obeys of the formula of calculation of precision of location in PEPT which is:
where, NF = fN is the number of gamma ray paths used in the final calculation after corrupt events have been discarded and σ is the standard deviation of the N detection. Also too large a value of f corresponds to including some corrupt events. Figure 4 shows that only about 15% of data are corrupt events. This is may be due to the septa in ECAT scanner which is effectively reducing scatter events. The result shows that for a point source using the optimum value, the accuracy of location for N = 250 is 0.6 mm for 3D and for each direction is around Δx = 0.35 mm, Δy = 0.37 mm and Δz = 0.30 mm.
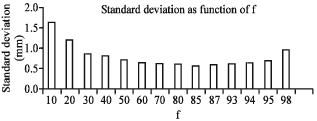 | |
| Fig. 4: | Variation of σ versus f |
 | |
| Fig. 5: | A turntable with a point source |
Another PEPT test was performed for a point source on a turntable rotating at 3.4 rev sec-1 (particle speed 2 m sec-1). This study was performed with using an 18F point source which its activity was approximately 37 MBq. The radius of turntable was 75 mm. Figure 5 shows the rotating point source on the turntable.
Figure 6 shows a short section of results from a tracking run with a tracer on turntable from which approximately 70 k events sec-1 were recorded. Consequently the locations were derived with N = 250 events and different fractions of trajectories and the best result were obtained when the f was selected 70%. The uncertainty in location (Δ) was given by the root-mean square (r.m.s) deviation of the locations from the fitted sinusoidal curves. For this point source which giving 70 k events sec-1 at a speed of about 2 m sec-1 approximately 270 PEPT locations were obtained per second. This means that a tracer particle can be tracked with a speed of 2 m sec-1 with an accuracy of 1.3 mm in 1D, 1.9 mm in 2D (xy plane) and 2.0 mm in 3D.
New frame: The configuration of the ECAT scanner suggests that it could be rebuilt in a flexible geometry for PEPT studies. For this purpose a frame was designed consisting of two rectangular arrays of shelves, each supporting two buckets, where the vertical position of each shelf can be adjusted. Two photos of this frame is shown in Fig. 7.
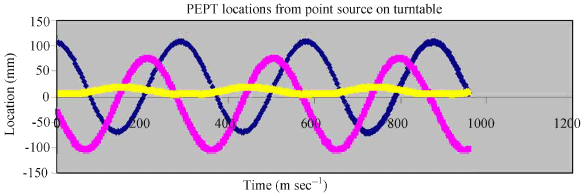 | |
| Fig. 6: | PEPT data for a tracer on a turntable rotating in the xy plane at 2 m sec-1 |
 | |
| Fig. 7: | Two photos of frame |
 | |
| Fig. 8: | Sensitivity regions, vertical profile (left), horizontal profile (right) |
Each half supports two columns of buckets with a centre to centre spacing of 380 mm, corresponding to a gap of approximately 180 mm between buckets. The shelves were configured giving a vertical centre to centre spacing between buckets of 100 mm, corresponding to a gap of approximately 44 mm between buckets. Initial trials used only 14 buckets, with four pairs mounted on one half frame and three pairs on the other. Figure 8 and 9 show two photos of sensitivity regions of vertical and horizontal axis, respectively.
First PEPT Test on ECAT Scanner at new frame: When the buckets were mounted in new frame, the PEPT software was modified to recognize the geometry of the modular camera. This has been done with ignoring the curvature of the blocks within each bucket. Nevertheless, reliable tracking has been achieved.
 | |
| Fig. 9: | Variation of σ versus f |
 | |
| Fig. 10: | Point source on turntable |
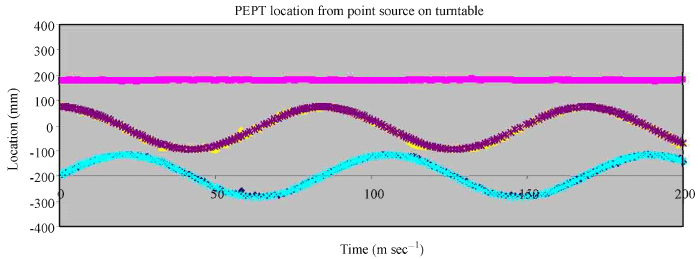 | |
| Fig. 11: | PEPT data for a tracer on a turntable rotating in the xy plane at 6 m sec-1 |
The first PEPT study was performed by using a stationary point source (18F) which was mounted on the level of buckets 2 and 18 in array 1 (corresponding 10 and 26 in array 2) in position N (near the central vertical axis). The coincidence data were recorded in buffers and a PEPT algorithm estimate of the position of the tracer particle. Figure 9 shows the variation of standard deviation, which was calculated by using the position of tracer, versus variety of f.
As shown in the Fig. 11 only less than 10% of data are corrupt events. So it appears that even with the septa removed less than 10% of events are corrupt for this bare point source. This result is similar to the stationary point source (Fig. 4) for which the best value for standard deviation was obtained around f = 85%. As is shown in Fig. 9 the accuracy on location (Δ) is about 1 mm which is worse than the value was obtained in Fig. 4 (0.6 mm). This is presumably because buckets are not accurately aligned so the positioning of buckets was not accurate. The result shows that for a point source using the optimum value, the accuracy of location for N = 250 is 1 mm for 3D and for each direction is around Δx = 0.2 mm, Δy = 0.3 mm and Δz = 0.8 mm. The main difference is the much poorer accuracy in the z coordinate (0.8 mm) due to the difficulty in determining how far the source is between the frames. In the ring geometry the accuracy is much more isotope. This is probably because the buckets were not accurately aligned on the frame. Another PEPT test was performed for a point source on a turntable rotating at 12 rev sec-1 (particle speed 6 m sec-1). This study was performed with using an 18F point source which its activity was approximately 10 MBq. Figure 10 shows the rotating point source on the turntable.
Figure 11 shows a short section of results from a tracking run with a tracer on turntable from which approximately 110 k events sec-1 were recorded.
Consequently the locations were derived with N = 250 events and different fractions of events and the best result were obtained when the f was selected 40%. The uncertainty in location (Δ) was given by the root-mean square (r.m.s) deviation of the locations from the fitted sinusoidal curves. For this point source which giving 110 k events sec-1 at a speed of about 12 m sec-1 approximately 450 PEPT locations were obtained per second. This means that a tracer particle can be tracked with a speed of 12 m sec-1 with an accuracy of 1.6 mm in 1D, 3.2 mm in 2D (xy plane) and 3.7 mm in 3D.
Compare of this result with the result of point source on a rotating turntable at original configuration shows that in new frame more events are corrupted. This is due to remove septa and the point source was not generally at the centre of the field of view between two buckets. But for both of them there is an optimum f for which the standard deviation is minimized as was expected by PEPT algorithm (Eq. 1). It should be noted that for the original configuration the standard deviation is considerably better than of the new frame. This error can be limited by accuracy in positioning the buckets on the frame and intrinsic precision of the system.
CONCLUSION
The initial results from the reconfigured ECAT931 show its potential as an extremely valuable tool for PEPT studies of a wide range of phenomena. The above results on a new frame have been obtained using just 14 buckets out of the possible 32 buckets. With further improvements to the PEPT algorithm and reducing the gaps between buckets as much as possible, it should be possible to achieved significantly better tracking.
ACKNOWLEDGMENT
A. Sadrmomtaz would like to record his gratitude to the Iranian Science Research and Technology Ministry for supporting him financially over the last three years.
REFERENCES
- Parker, D.J., C.J. Broadbent, P. Fowles, M.R. Hawkesworth and P.A. McNeil, 1993. Positron emission particle tracking-a technique for studying flow within engineering equipment. Nucl. Instrum. Methods Phys. Res. Sect. A: Acceler. Spectrom. Detect. Assoc. Equip., 326: 592-607.
CrossRefDirect Link - Parker, D.J., M.R. Hawkesworth, C.J. Broadbent, P. Fowles, T.D. Fryer and P.A. McNeil, 1994. Industrial positron-based imaging: Principles and applications. Nucl. Instrum. Methods Phys. Res. Sect. A: Acceler. Spectrom. Detect. Assoc. Equip., 348: 583-592.
CrossRefDirect Link - Parker, D.J., M.R. Hawkesworth and T.D. Beynon, 1995. Process applications of emission tomography. Chem. Eng. J. Biochem. Eng. J., 56: 109-117.
CrossRefDirect Link - Parker, D.J., R.N. Forster, P. Fowles and P.S. Takhar, 2002. Positron emission particle tracking using the New Birmingham Positron camera. Nuclear Instruments Methods Phys. Res. A, 477: 540-545.
Direct Link








