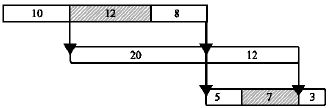
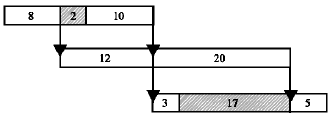
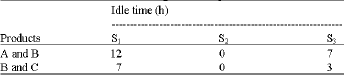
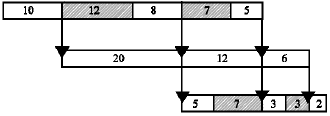
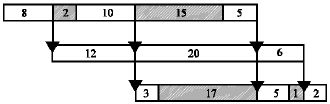
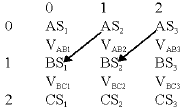
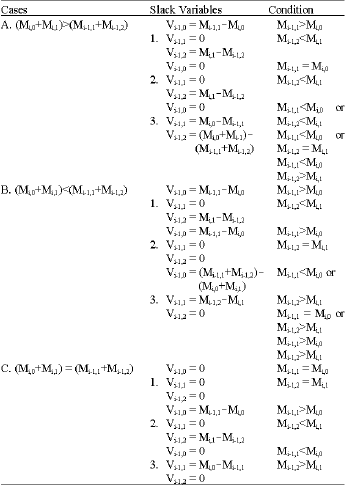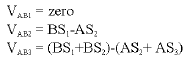Research Article
Determination of Inter-Stage Idle Times in Scheduling Design of a Three Stage Zero Wait Batch Process
Department of Chemical Engineering, Universiti Teknologi Petronas,31750 Tronoh, Perak Darul Ridzuan, Malaysia
M.I. Abdul Mutalib
Department of Chemical Engineering, Universiti Teknologi Petronas,31750 Tronoh, Perak Darul Ridzuan, Malaysia
K.A. Amminudin
Department of Chemical Engineering, Universiti Teknologi Petronas,31750 Tronoh, Perak Darul Ridzuan, Malaysia
Ayyaz Muhammad
Department of Chemical Engineering, Universiti Teknologi Petronas,31750 Tronoh, Perak Darul Ridzuan, Malaysia