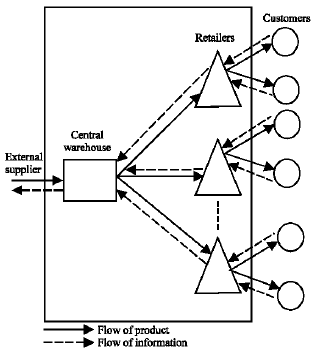
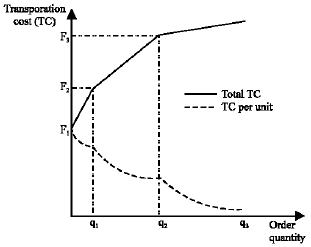
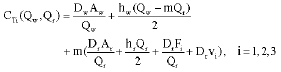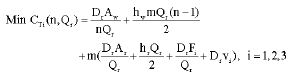Research Article
A Search Algorithm for Determination of Economic Order Quantity in a Two-Level Supply Chain System with Transportation Cost
Department of Industrial Engineering, Sharif University of Technology, Tehran, Iran
Rasoul Haji
Department of Industrial Engineering, Sharif University of Technology, Tehran, Iran