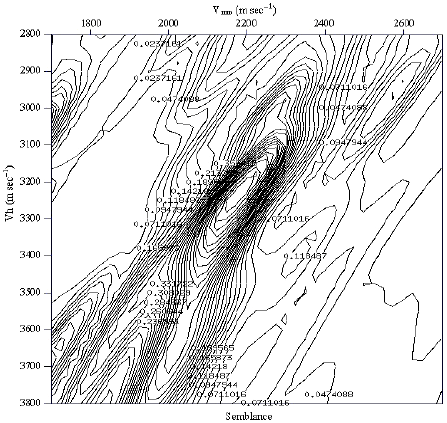
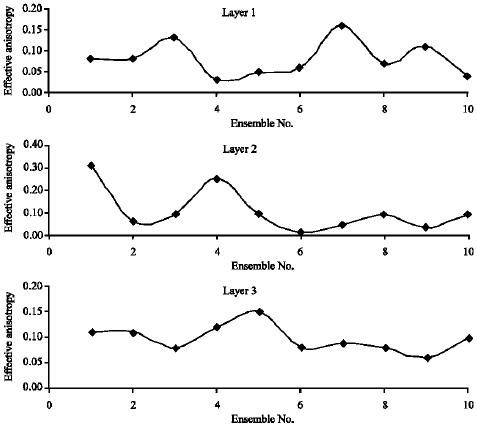
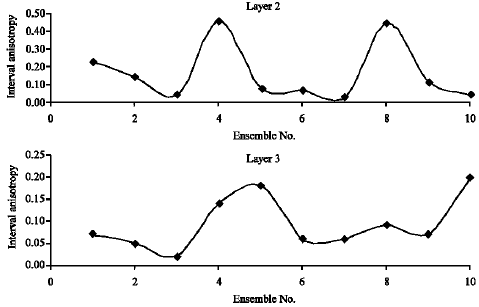
Research Article
Anisotropy Parameter Estimation Using Semblance Based Rational Interpolation Technique
Department of Geology and Physics, Niger Delta University, Wilberforce Island, Bayelsa State, Nigeria
Kingsley D. Alagoa
Department of Geology and Physics, Niger Delta University, Wilberforce Island, Bayelsa State, Nigeria
Etim D. Uko
Department of Physics, Rivers State University of Science and Technology, Port Harcourt, Nigeria