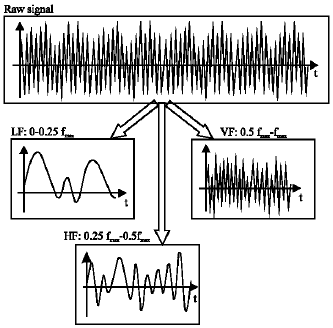
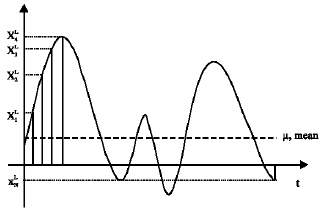
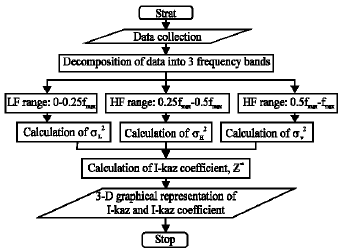
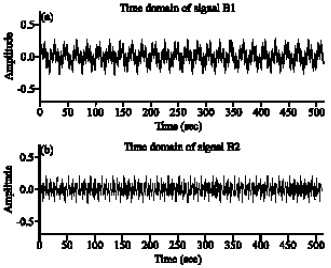
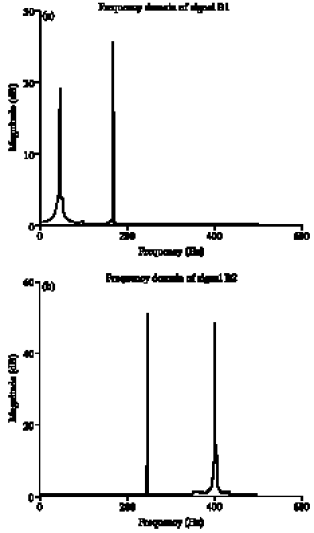
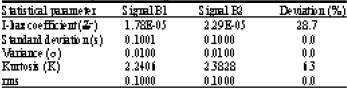
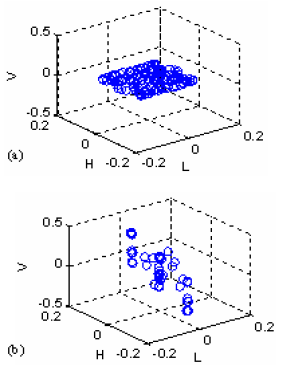
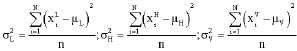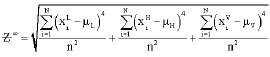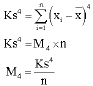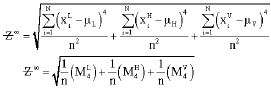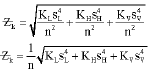Research Article
Development of Integrated Kurtosis-Based Algorithm for Z-Filter Technique
Department of Mechanical and Materials Engineering,Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia
M.J. M. Nor
Department of Mechanical and Materials Engineering,Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia
N. Jamaludin
Department of Mechanical and Materials Engineering,Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia
S. Abdullah
Department of Mechanical and Materials Engineering,Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia
F. Lamin
Department of Mechanical and Materials Engineering,Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia
C.K. E. Nizwan
Department of Mechanical and Materials Engineering,Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia