Research Article
River Flow Forecasting Using Neural Networks and Auto-Calibrated NAM Model with Shuffled Complex Evolution
Department of Civil Engineering, Tarbiat Modarres University, Tehran, Iran
M. Ghodsian
Department of Civil Engineering, Tarbiat Modarres University, Tehran, Iran
S.A.A. Salehi Neishabouri
Department of Civil Engineering, Tarbiat Modarres University, Tehran, Iran
M. Shakiba
Department of Electrical Engineering, K.N. Toosi University of Technology, Tehran, Iran









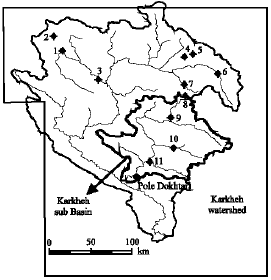
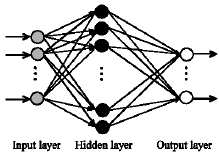
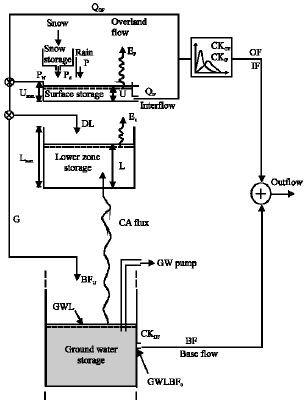

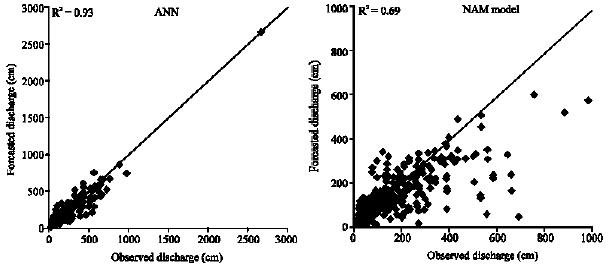
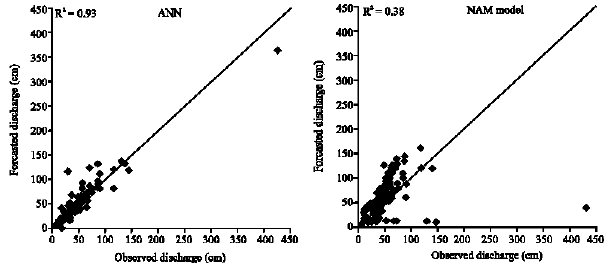
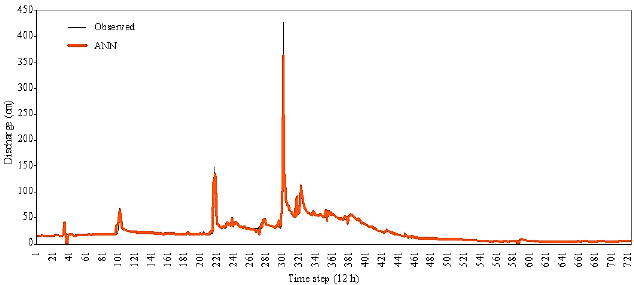
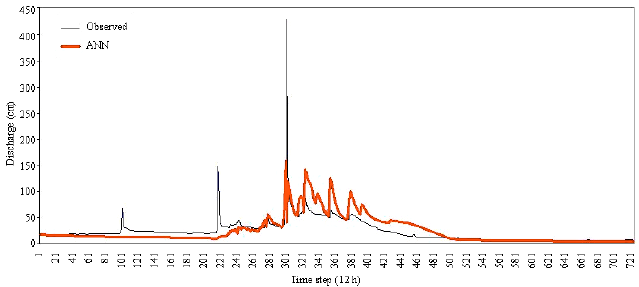
Kassu Jilcha Reply
I saw the abstract and really I appreciated your work. I would like to add extra works using the Neural network application