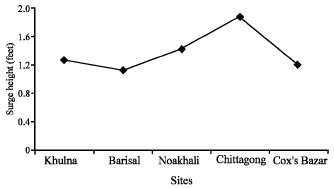
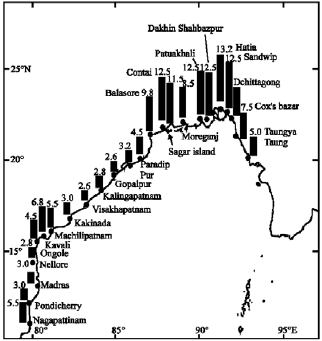
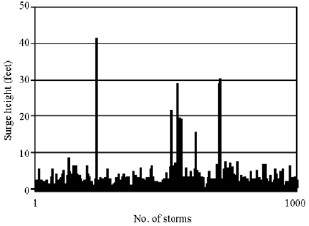
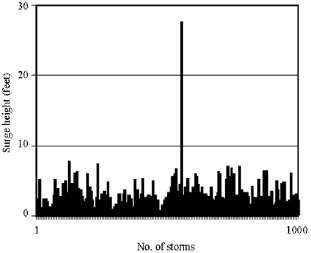
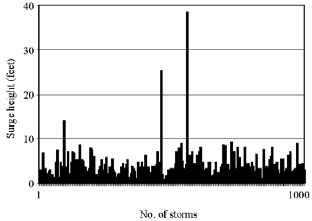
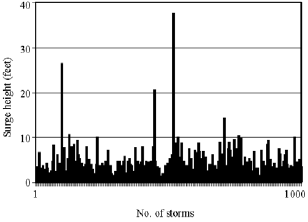
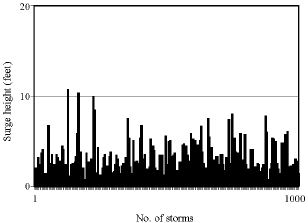
Research Article
Tropical Cyclone Wind Characteristics for the Bangladesh Coast Using Monte Carlo Simulation
Center for Texas Beaches and Shores, Texas A and M University-Galveston, 5007 Avenue U, Galveston, Texas 77551, USA
Richard E. Peterson
Atmospheric Science Group, Texas Tech University, Lubbock, Texas 79409, USA