ABSTRACT
This study deals with the two-variable Hermite matrix polynomials, some relevant matrix functions appear interims of the two-variable Hermite matrix polynomials the relationships with Hermite matrix polynomials of one variable, Chepyshev matrix polynomials of the second kind have been obtained and expansion of the. Gegenbauer matrix polynomials as series of Hermite matrix polynomials.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.1221.1227
URL: https://scialert.net/abstract/?doi=jas.2008.1221.1227
INTRODUCTION
Laguerre, Hermite and Gegenbauer matrix polynomials were introduced and studied (Defez and Jo’dar, 1998; Msayyed et al., 2004; Jo’dar et al., 1994), for matrix in CN×N. Moreover, some properties of the Hermite matrix polynomials are given (Defez and Jo’dar, 1998; Defez et al., 2002) and a generalized form of the Hermite matrix polynomials has been introduced and studied in (Msayyed et al., 2003).
Jo’dar and Company (1996) introduced the class of Hermite matrix polynomials Hn (x, A) which appear as finite series solutions of second order matrix differential equations Y"-xAY+nAY = 0, for a matrix A in CN×N whose eigen values are all in right open half-plane. If A is a matrix in CN×N, it spectrum σ(A) denotes the set of all eigenvalues of A. If f(z), g(z) are holomorphic functions in an open set Ω of the complex plane and if σ(A)⊂dΩ we denote by f(A), g(A), respectively, the image by the Riesez-Dunford functional calculus of the functions f(z), g(z), respectively, acting on the matrix A and
f(A) g(A) = g(A) f(A)
If Do is the complex plane cut along the negative real axis and log(z) denotes the principal logarithm of z, then z1/2 represents exp(1/2log(z)). If A is a matrix in CN×N with σ(A)⊂dDo then A½=![]() denotes the image by z½ of the matrix functional calculus acting on the matrix A.
denotes the image by z½ of the matrix functional calculus acting on the matrix A.
Let A is a matrix in CN×N such that,
| (1) |
then nth Hermite matrix polynomial Hn (x, A) is defined by Jo’dar and Company (1996)
| (2) |
and the following Rodrigues formula holds
| (3) |
and satisfy the three terms recurrence relation ship.
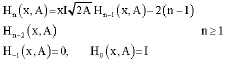 | (4) |
where, I is the identity matrix in CRxR.
by Jo’dar and Company (1996) we also have
| (5) |
Batahan (2006) define the two-variable Hermite matrix polynomials by
| (6) |
and satisfy the recurrence relation ship.
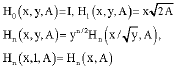 | (7) |
where, Hn (x, A) is defined in (2)
we shall use the relations (Defez and Jo’dar, 1998; Jo’dar and Company, 1996)
| (8) |
| (9) |
where, A (k, n) is a matrix on CN×N and the relation (Msayyed et al., 2004)
| (10) |
Khan and Abukahmmash (1998) obtained the generating function for Hn (x, y) by
| (11) |
for the Hermite polynomials of two variables
| (12) |
where, Hn (x) is the well known Hermite polynomial of one-variable and it’s equivalent to the following explicit representation of Hn (x, y) by
| (13) |
Kahmmash (2007) define Gegenbauer matrix polynomials of two variables by
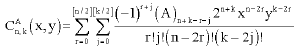 | (14) |
where, ![]() (x,y) is a polynomial in two variables x and y of degree n in x and k in y thus
(x,y) is a polynomial in two variables x and y of degree n in x and k in y thus![]() (x,y) is a polynomial in two variables x and y of degree n+k.
(x,y) is a polynomial in two variables x and y of degree n+k.
The aim of this study is to establish the two variable extension of the Hermite matrix polynomials and the generating function for these matrix polynomials and Rodrigues formula, expansion series of Hermite matrix polynomials. Chepyshev matrix polynomial of the second kind and expansion of the Gegenbauer matrix polynomials as series of Hermite matrix polynomials.
HERMITE MATRIX POLYNOMIALS OF TWO VARIABLES
Let A be a matrix in CN×N satisfying the condition (1). we define two variable Hermite matrix polynomials by
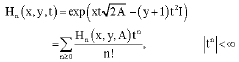 | (15) |
we can write,
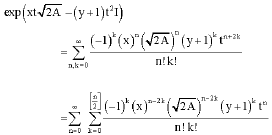 | (16) |
| (17) |
for y = 0, (17) reduces to Hermite matrix polynomial Hn (x, A) of one variable (Jo’dar and Company, 1996)
RECURRENCE RELATIONS
Now, since
| (18) |
differentiating (18) partially w.r.t. y, we get
| (19) |
| (20) |
which with a shift of index on left yields,
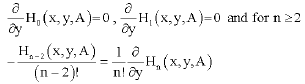 | (21) |
iteration of (21), gives
| (22) |
differentiating (22) partially w.r.t. x, we get.
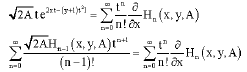 | (23) |
which with a shift of index on left yields,
 |
or
| (24) |
iteration of (24), gives
| (25) |
from (20), we get
| (26) |
let k = 2, in (25), we get
(26), yields
| (27) |
Equation 22, 25 and 27 are similar to the results given by Batahan (2006) differentiating (18) partially w.r.t. wt, we get.
| (28) |
multiplying (23), (19) and (28), by ![]() 2y and -t, respectively and adding, we get
2y and -t, respectively and adding, we get
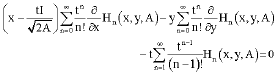 |
or
 |
equating the coefficients of tn, we get
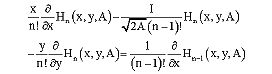 |
or
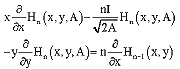 | (29) |
combination of (24), (26) and (29) yields
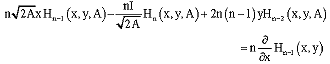 | (30) |
from (29) and (30) we obtain the pure recurrence relation
 | (31) |
from (24) and (29) the partial differential Equation given by
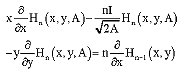 |
or
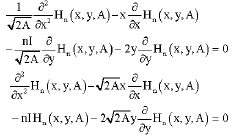 | (32) |
RELATIONSHIPS BETWEEN
Hn (x, y, A) AND Hn (x, A)
Since,
| (33) |
where, Hn (x, A) is well known Hermite matrix polynomial of one variable (Jo’dar and Company, 1996) replacing x by ![]() and t by
and t by ![]() in (33), we get
in (33), we get
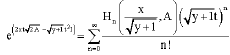 | (34) |
in view of (15), we get
 |
equating coefficients of t", we get
| (35) |
now
| (36) |
for y = 0, (35) reduces
| (37) |
and for x = 0, we get
| (38) |
for x = y = 0, we get
| (39) |
THE RODRIGUES FORMULA
Examination of the defining relation
| (40) |
in the light of maclaurin’s theorem gives us at once.
| (41) |
the function ![]() is independent of t. So we may write
is independent of t. So we may write
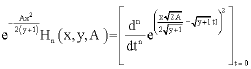 |
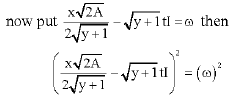 |
or
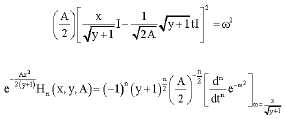 |
or
| (42) |
a formula of the same nature as Rodrigue’s formula for Hermite matrix polynomial of one variablenote, setting y = 0 in (42) it gives the Rodrigue’s formula (Jo’dar and Company, 1996) of Hn = (x, A),
EXPANSION OF TWO-VARIABLES HERMITE MATRIX POLYNOMIALS
Since
| (43) |
it follows that
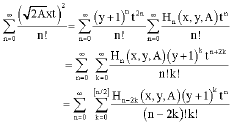 |
equating coefficients of tn, we get
| (44) |
for y = 0, (44), gives the expansion of one variable Hermite matrix polynomials (Defez and Jo’dar, 1998).
THE CHEPYSHEV MATRIX POLYNOMIALS
The two-variable Hermite matrix polynomials will be exploited here to define a matrix Version of Chepyshev polynomials. The Chepyshev polynomials of the second kind (Davis, 1975) are defined by
| (45) |
suppose that A is a matrix in CN×N satisfying the condition (1), by (16) it follows that
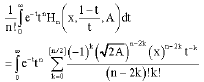 |
since the summation in the right-hand side of the above equality is finite, then the series and the integral can be permuted. also, in view of
we can write
| (46) |
hence, the chepyshev matrix polynomials of the second kind can be defined by
or by using the two-variable Hermite matrix polynomials in the form
in similar way, we define the generalized Chepyshev matrix polynomials of the second kind as follows
and
it’s evident that
| (47) |
EXPAND THE GEGENBAUER MATRIX POLYNOMIALS OF TWO VARIABLES IN SERIES OF Hn (x, y, A)
Let us now employ (14), (9) and (44) and taking into account that each matrix commutes with it self.
from (14), one gets
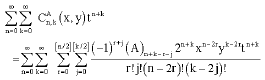 | (48) |
which on applying (9) becomes.
From (44), we get
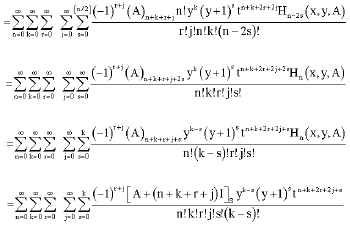 |
by (10) it follows that
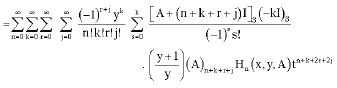 |
we may write as
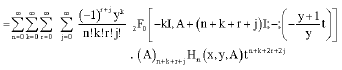 |
again from (9), one gets
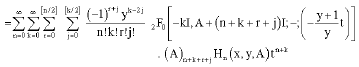 |
equating the coefficient of tn+k we obtain an expansion of the two-variable Gegenbauer matrix Polynomials as series of two-variable Hermite matrix polynomials in the form
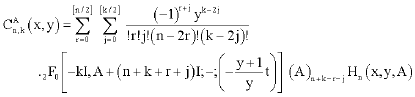 | (49) |
REFERENCES
- Batahan, R.S., 2006. Anew extension of Hermite matrix polynomials and its applications. Linear Algebra Appl., 419: 82-92.
CrossRefDirect Link - Defez, E. and L. Jodar, 1998. Some application of the hermite matrix polynomials series expansions. J. Comput. Applied Math., 99: 105-117.
CrossRef - Jodar, L., R. Company and E. Navarro, 1994. Laguerre matrix polynomials and systems of second order differential equations. Applied Numer. Math., 15: 53-63.
CrossRef - Jodar, L. and R. Company, 1996. Hermite matrix polynomials and second order matrix differential equations. J. Anal. Theory Appl., 12: 20-30.
Direct Link - Kahmmash, G.S., 2007. A study of a two variables gegenbauer matrix polynomials and second order matrix partial differential equations. Int. J. Math. Anal., 2: 807-821.
Direct Link - Sayyed, K.A.M., M.S. Metwally and R.S. Batahan, 2003. On generalized Hermite matrix polynomials. Elect. J. Linear. Algebra, 10: 272-279.
Direct Link - Msayyed, K.A., M.S. Metwally and R.S. Bataha, 2004. Gegenbauer matrix polynomials and order matrix differential equations. Divulgaciones Matematics, 12: 101-115.
Direct Link








