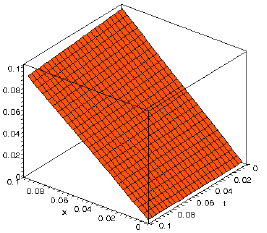
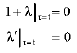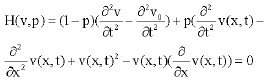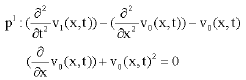Research Article
Variational Iteration Method and Homotopy-Perturbation Method for Solving Different Types of Wave Equations
1,3Department of Civil and Mechanical Engineering, Mazandaran University of Technology, P.O. Box 484, Babol, Iran
Abdoul R. Ghotbi
2Department of Civil Engineering, Shahid Bahonar University, Kerman, Iran
F. Farrokhzad
1,3Department of Civil and Mechanical Engineering, Mazandaran University of Technology, P.O. Box 484, Babol, Iran
D.D. Ganji
1,3Department of Civil and Mechanical Engineering, Mazandaran University of Technology, P.O. Box 484, Babol, Iran