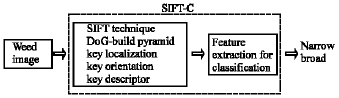
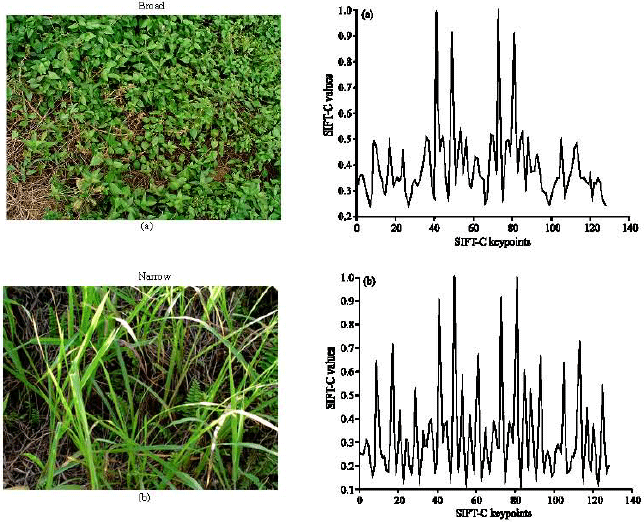
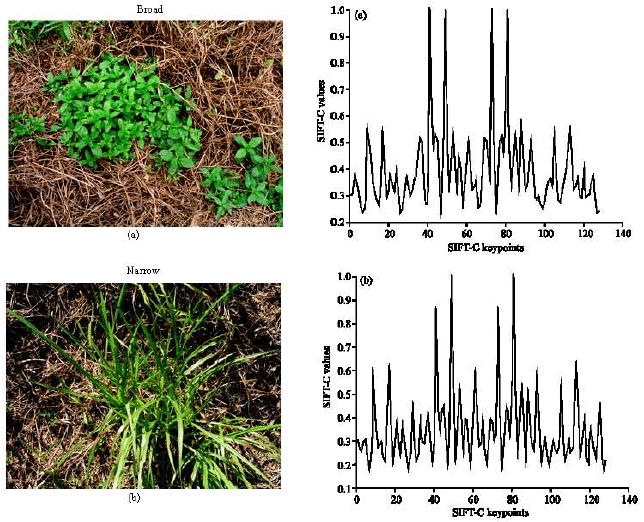
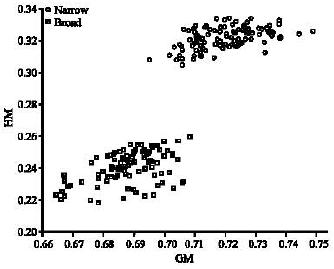
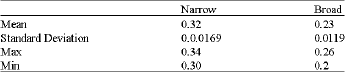
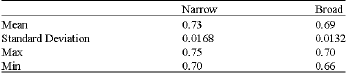
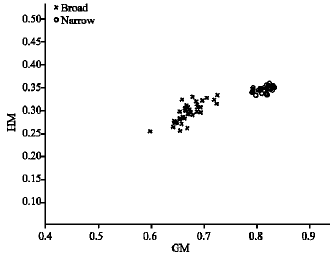
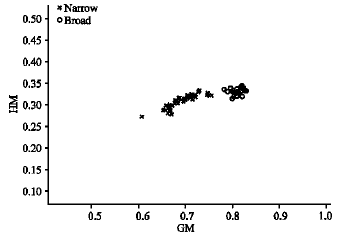
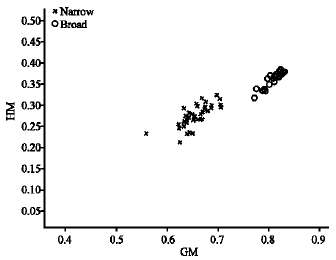
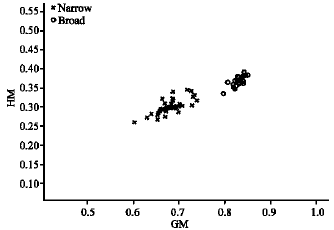
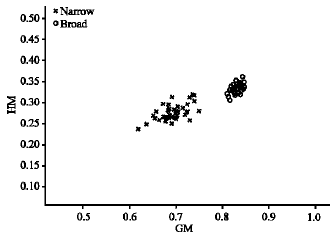
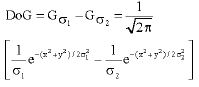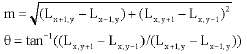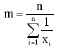Research Article
Scale Invariant Feature Transform Technique for Weed Classification in Oil Palm Plantation
Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia
Mohd. Marzuki Mustafa
Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia
Aini Hussain
Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600, Bangi, Selangor, Malaysia
Saifudin Razali
Faculty of Electrical and Electronic Engineering, Universiti Malaysia,Pahang, 25000 Kuantan, Pahang, Malaysia