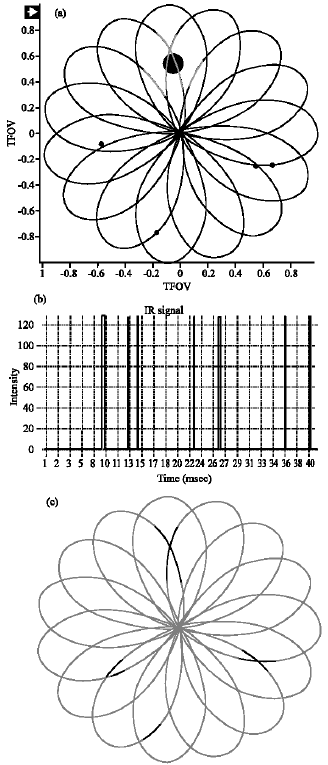
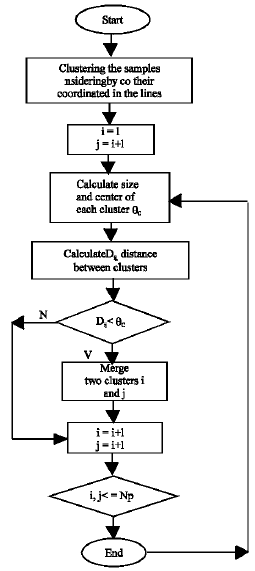
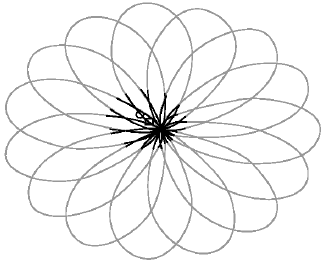
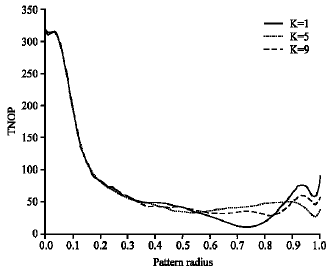
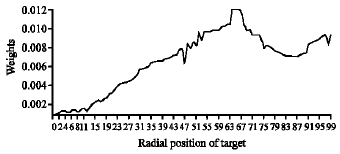
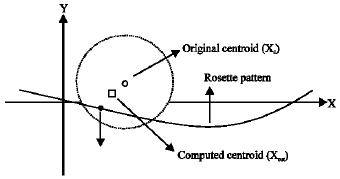
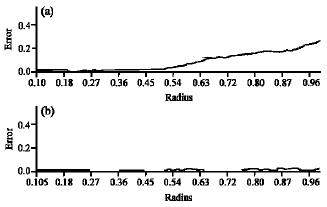
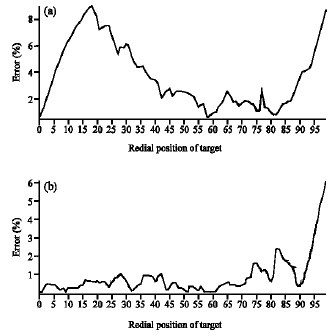
Research Article
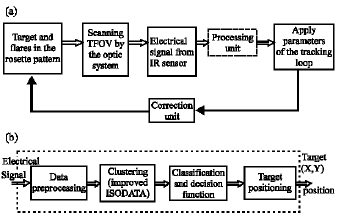
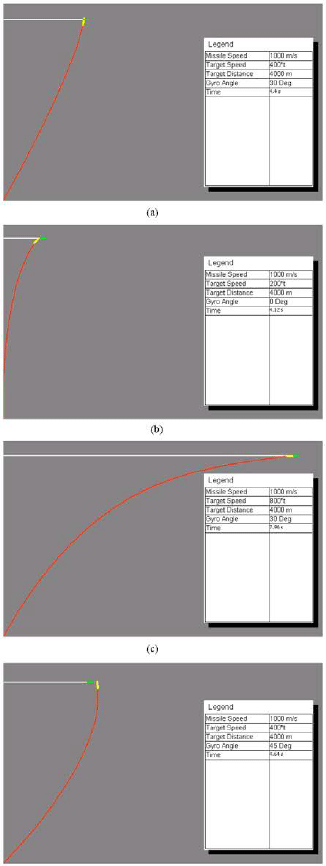
Increasing Accuracy of Tracking Loop for the Rosette Scanning Seeker Using Improved ISODATA and Intelligent Center of Gravity
Department of Electrical Engineering, Iran University of Science and Technology,Narmak, 16846, Tehran, Iran
Shahriar Baradaran Shokouhi
Department of Electrical Engineering, Iran University of Science and Technology,Narmak, 16846, Tehran, Iran