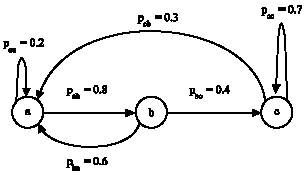
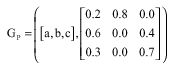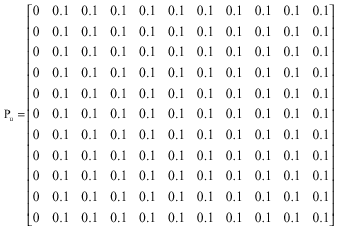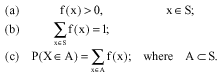Research Article
Mathematical Discussions About Data Oriented Modeling of Uniform Random Variable
Islamic Azad University, Tabriz Branch, Tabriz, Iran, IAUT-CRL
Mehdi Naghian Fesharaki
Malek-Ashtar University of Technology, Tehran, Iran
Mirkamal Mirnia
Islamic Azad University, Tabriz Branch, Tabriz, Iran, IAUT-CRL
Mohammad Teshnehlab
Khaje Nasir Toosi University of Technology, Tehran, Iran