ABSTRACT
In this study, the problem of peristaltic flow through a porous medium is studied for the case of non-uniform channel. The problem is formulated and analyzed using a perturbation series of a wave number as a parameter. We obtained an explicit form for the velocity components and the pressure gradient to the second order. Moreover, the pressure rise and the average pressure rise are computed and are explained graphically. The results show that both pressure rise and average pressure rise decrease as permeability parameter k increases.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.1085.1090
URL: https://scialert.net/abstract/?doi=jas.2008.1085.1090
INTRODUCTION
Peristalsis is a mechanism of pumping fluids in a tube by means of a contractile ring around the tube which pushes the fluid forward. By peristaltic pumping we mean transporting the fluid by a wave of contraction or expansion from a region of lower pressure to higher pressure.
The problem of peristaltic flow in uniform and non uniform channel has been studied by many authors for both Newtonian and non Newtonian fluids. Some of these studies have been done by Abd El Naby et al. (2004), Elshehawey and Husseny (2002), Mekheimer (2005), Mishra and Ramachandra (2003), Misra and Pandey (2001) and Elshehawey and Sobh (2001).
Recently, some studies have been done to understand the influence of an inserted endoscope on peristaltic motion of some types of fluids. Some of these studies were made by Abd El Naby and El Misery (2002) and El Misery et al. (2003).
The effect of the porous medium on peristaltic transport of a Generalized Newtonian fluid in a uniform planar channel has been studied by Elshehawey et al. (2000). Also, Sobh (2004) studied the peristaltic transport of a magneto-Newtonian fluid through a porous medium in uniform channel. It has been shown that the pressure rise increases as the permeability decreases.
Since peristalsis is now well known to physiologists to be one of the major mechanisms for fluid transport in many biological systems and most biological organs are generally observed to be non-uniform, we purpose to study the effect of porous medium on peristaltic motion of a Newtonian fluid in a non-uniform channel.
Because of the complexity of the governing equations, we shall consider the case of creeping flow. The problem is formulated and a perturbation solution with wave number as a parameter is obtained to second order. The velocity field and pressure gradient are obtained in explicit forms. Also, the pressure rise per unit wavelength is computed numerically and is plotted with the variation of the time. Moreover, the average pressure rise is graphed versus flow rate for various values of permeability parameter k.
FORMULATION AND ANALYSIS
Consider the two dimensional flow of an incompressible Newtonian fluid in an infinite channel of non-uniform thickness with a sinusoidal wave traveling down its wall. The geometry of the wall surface is defined as:
(1) |
With
(2) |
where,![]() is the half width of the channel at any axial distance from the inlet, a is the half width of the channel at the inlet, K1<<1 is constant whose magnitude depends on the length of the channel and exit and inlet dimensions, b the is the amplitude of the wave, λ is the wavelength, c is propagation velocity of the wave, t is the time.
is the half width of the channel at any axial distance from the inlet, a is the half width of the channel at the inlet, K1<<1 is constant whose magnitude depends on the length of the channel and exit and inlet dimensions, b the is the amplitude of the wave, λ is the wavelength, c is propagation velocity of the wave, t is the time.
In the moving coordinates![]() which travel in the
which travel in the ![]() direction with the same speed as the wave, the flow is steady but in the fixed coordinates, the flow in the channel can be treated as unsteady. The coordinate frames are related through (Shapiro et al., 1969).
direction with the same speed as the wave, the flow is steady but in the fixed coordinates, the flow in the channel can be treated as unsteady. The coordinate frames are related through (Shapiro et al., 1969).
(3) |
(4) |
where, ![]() and
and ![]() are the velocity components in the fixed and the moving frames, respectively.
are the velocity components in the fixed and the moving frames, respectively.
Using the following non-dimensional parameters
![]()
and
(5) |
where, δ is the wave number, Re is the Reynolds number,and φ is the amplitude ratio, φ = b/a<1, the non-dimensional equations of motion are:
(6) |
(7) |
(8) |
Considering the creeping flow (Re = 0), taking into account that δ is small and eliminating the pressure from Eq. 7 and 8, we obtain the following system of differential equations:
(9) |
(10) |
with the continuity Eq. 6.
The nom-dimensional boundary conditions are:
(11a) |
(11b) |
RATE OF VOLUME FLOW
The instantaneous volume flow rate in the stationary frame is given by:
(12) |
where,![]() is a function of
is a function of ![]() and
and ![]() .
.
On substituting Eq. 3 and 4 into Eq. 12 and then integrating, one finds:
(13) |
Where:
(14) |
is the rate of volume flow in the moving frame (wave frame) and independent of time. Here![]() is a function of
is a function of ![]() only.
only.
The time-mean flow over a period T = λ/c at a fixed position is defined as:
(15) |
Substituting from Eq. 13 into Eq. 15 and using Eq. 1 and integrating, we obtain
(16) |
Defining the dimensionless time-mean flows Θ and F as follows:
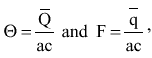 | (17) |
Equation 16 can be rewritten as:
(18) |
Where:
(19) |
METHOD OF SOLUTION
We expand the following quantities in a power series of the small parameter δ as follows:
![]()
![]()
(20) |
The use of expansions (20) with Eq. 6, 9, 10 and 11 gives the following systems:
System of order zero
(21) |
(22) |
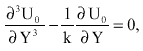 | (23) |
With the dimensionless boundary conditions
(24a) |
(24b) |
The solution of this system for U0 subject to the boundary conditions is:
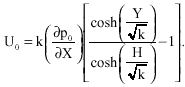 | (25) |
The instantaneous volume flow rate F0 in the moving coordinates is given by:
![]()
which implies that
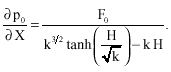 | (26) |
Using Eq. 21, 25 and 26, we obtain the alternative form of U0 and V0 as:
(27a) |
(28b) |
Where:
![]()
and
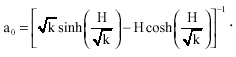 | (29) |
System of order one: Equating the coefficients of δ on both sides in Eq. 6, 9, 10 and 11, we get
(30) |
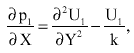 | (31) |
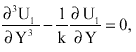 | (32) |
with the boundary conditions
(33a) |
(33b) |
Solving this system for U1, after using Eq. 27, we obtain
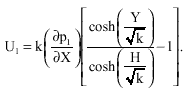 | (34) |
Again, the alternative form for U1, in which ∂p1/∂X is replaced by an equivalent expression in term of F1, is given by:
(35) |
Where:
(36) |
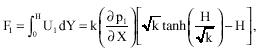
and
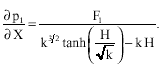 | (37) |
Using the continuity equation, one finds
(38) |
System of order two: Equating the coefficients of δ2 on both sides in Eq. 6, 9, 10 and 11, we get
(39) |
(40) |
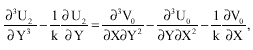 | (41) |
with the boundary conditions
(42a) |
(43b) |
Solving this system for U2, after using Eq. 27, we obtain
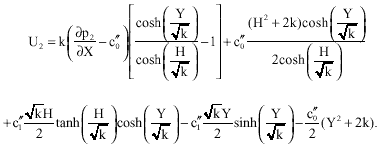 | (44) |
The instantaneous volume flow rate F2 is given by:
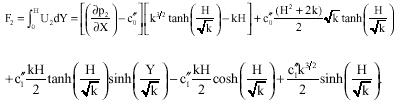
Solving the above equation for ∂p2/∂X, we get
![]()
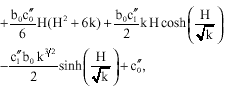 | (45) |
Where:
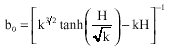 | (46) |
Substituting Eq. 45 into Eq. 44 we obtain the alternative form of U2 as:
(47) |
Where:
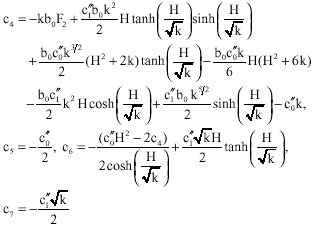 | (48) |
Now, the axial velocity component U and the pressure gradient can be expressed, to second order where F0 = F-δ F1-δ2 F2, as:
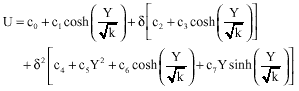 | (49) |
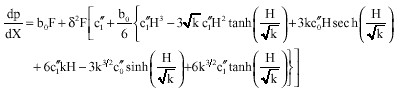 | (50) |
The pressure rise per wave length Δpλ(t) is given by:
(51) |
RESULTS AND DISCUSSION
It is clear that we have obtained analytical form, to second order of δ, for the velocity field and the pressure gradient, Eq. 49 and 50. As k tends to infinity, we obtainthe velocity field and the pressure gradient of peristaltic flow of Newtonian fluid in non-uniform channel.
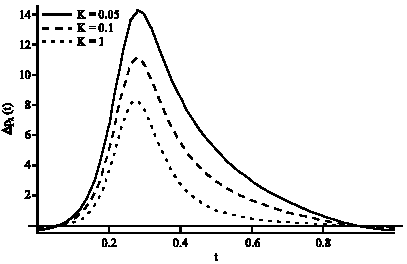 | |
| Fig. 1: | The pressure rise versus the time at δ = 0.02, φ = 0.8 and Θ = 0 |
| |
| Fig. 2: | The pressure rise versus the time at δ = 0.02, φ = 0.8 and Θ = 0.1 |
We shall now compute the dimensionless pressure rise Δpλ(t) over the channel length for different values of the dimensionless flow rate Θ and permeability parameter k.
The average pressure rise is then evaluated by averaging Δpλ(t) over one period of the wave. As the integral in Eq. 51 is not integrable in the closed form, it is evaluated numerically using the MATHEMATICA package. Following Srivastava and Srivastava (1984), we take K1 = 3a/λ and then plot Eq. 51.
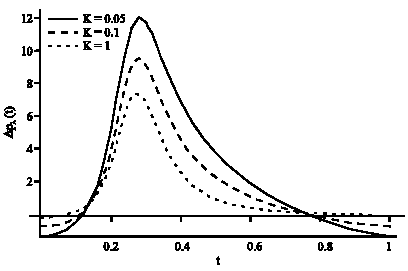
Figure 1-3 represent the variation of dimensionless pressure rise with the dimensionless time for δ = 0.02, φ = 0.8, (k = 0.05, 0.1, 1) and Θ = 0, 0.1 and 0.2, respectively. We have observed that the pressure rise decreases with increasing flow rate and becomes maximal at zero flow rate. Also, it is clear from these figures that the pressure rise decreases with increasing permeability parameter k. Also, the behavior of the pressure rise is the same for various values of flow rate Θ.
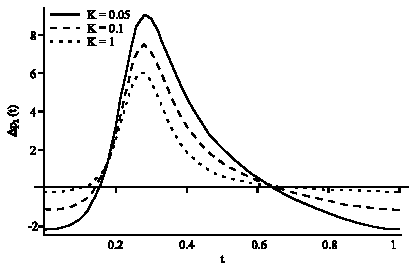 | |
| Fig. 3: | The pressure rise versus the time at δ = 0.02, φ = 0.8 and Θ = 0.2 |
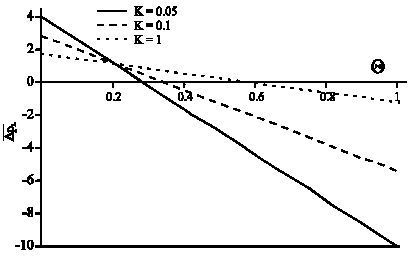 | |
| Fig. 4: | The average pressure rise versus flow rate at δ = 0.02 and φ = 0.8 |
The average pressure rise versus the flow rate is plotted in Fig. 4 for δ = 0.02, φ = 0.8, (k = 0.05, 0.1, 1). As shown, the average pressure rise decreases as the permeability parameter increases. This is because of the resistance caused by the porous medium.
REFERENCES
- Abd El Naby, A.H. and A.M. El Misery, 2002. Effects of an endoscope and generalized Newtonian fluid on peristaltic motion. Applied Math. Comput., 128: 19-35.
Direct Link - Abd El Naby, A.H., A.M. El Misery and M. Abd El Kareem, 2004. Separation in the flow through peristaltic motion of a Carreau fluid in uniform tube. Physica A. Stat. Mech. Appl., 343: 1-14.
Direct Link - El Misery, A.M., A. El Hakeem, A. El Naby and A.H. El Nagar, 2003. Effects of a fluid with variable viscosity and an endoscope on peristaltic motion. J. Phys. Soc. Jap., 72: 89-93.
Direct Link - Elshehawey, E.F., A.M. Sobh and E.M. Elbarbary, 2000. Peristaltic motion of a generalized Newtonian fluid through a porous medium. J. Phys. Soc. Jap., 69: 401-407.
Direct Link - Elshehawey, E.F. and A.M. Sobh, 2001. Peristaltic viscoelastic fluid motion in a tube. Int. J. Math. Math. Sci., 26: 21-34.
Direct Link - Elshehawey, E.F. and S.Z. Husseny, 2002. Peristaltic transport of a magneto-fluid with porous boundaries. Applied Math. Comput., 129: 421-440.
Direct Link - Mekheimer, K.H.S., 2005. Peristaltic transport of a Newtonian fluid through a uniform and non-uniform annulus. Arab. J. Sci. Eng., 30: 69-83.
Direct Link - Mishra, M. and A.R. Rao, 2003. Peristaltic transport of a Newtonian fluid in an asymmetric channel. Zeitschrift Angewandte Mathematik Physik, 54: 532-550.
Direct Link - Misra, J.C. and S.K. Pandey, 2001. Peristaltic flow of a multilayered power-law fluid through a cylindrical tube. Int. J. Eng. Sci., 39: 387-402.
Direct Link - Shapiro, A.H., M.Y. Jaffrin and S.L. Weinberg, 1969. Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech., 37: 799-825.
CrossRef - Srivastava, L.M. and V.P. Srivastava, 1984. Peristaltic transport of blood: Casson model-II. J. Biomech., 17: 821-829.
PubMed