Research Article
Production of Optimized DEM Using IDW Interpolation Method (Case Study; Jam and Riz Basin-Assaloyeh)
R.S. and GIS Centre, University of Mazandaran, P.O. Box 416, Babolsar, Iran
S. Modallaldoust
University of Mazandaran, Iran
INTRODUCTION
Topographic conditions of the watershed are one of the integrated physical factors which can be seen in nature. In other word, every part of the land characterized with an elevation which in most cases is more similar to the other points of the catchments, however using some indicated points as ground control points the other unknown point will identified. Estimation and assessment method of continuous variable value in area where there is no any experimental model and the ground control points are scattered, interpolation method can be used (Bob and Booth, 2000). In fact, interpolation method indicates the continuous spatial variations as identified surface. For the mentioned purpose IDW can be used in interpolation method. In this way, the value of each variable will be calculated base on neighbors mean in specific distance. So that, distance inverse is weighted from unknown points. The distance of unknown point's decreases from control points is related to their neighboring so the value weight of the nearest points will increase and unknown points will be estimated by use of surrounding points of a certain radius (Childs and Colin, 2004). When the power is zero, the distance's role can be ignored and unknown points reached from the neighbor points mean. While the power increases the distance affect would increase and closer distances reached to the higher weight. Usually, in IDW model is recommended to use a power higher than 1 (Meyers, 1994). The gained results layers of this method depend on searching radius and number of neighbor points which including the recent points. It can be decided to have an equal weight for the all directions and specified circle or ellipse which included unknown points in their center, if there is no any trend of direction for the remind data. The value of point which placed in ellipse which is not clear so it can be calculate using the existent points in ellipse. Then the space of every point will be measured. Finally the distance inverse will be computed according to the unknown pint so, the power obtains and its average will be considered for unknown points (Tali, 2004). In fact the power degree is a weight which is given to the related distances. Therefore, the point's distances increases from unknown point with lower weight in assessment of these points (Johnston and Kevin, 2001). A DEM is a numerical representation of topography, usually made up of equal-sized cells, each with a value of elevation. Its simple data structure and widespread availability have made it a popular tool for land characterization. Because topography is a key parameter controlling the function of natural ecosystems, DEMs are highly useful to deal with ever-increasing environmental issues. Since many GIS applications rely on DEMs, their intrinsic quality is critical, particularly for hydrologic modeling (Beven and Krikby, 1979; O’loughlin, 1986; Darboux et al., 2002) or soil distribution analysis (Bloschl and Sivalapan, 1995; Chaplot et al., 2000; Mc Bratney et al., 2003). The applications of DEMs are very diverse, ranging from basin characterization which requires the investigation of large areas, to the evaluation of water pounding capacity at the clod level that requires very accurate height estimates. The development of numerical representations of landscapes over large area with a high resolution DEM is thus one of the most important scientific challenges of environmental studies. Several factors affect the quality of DEMS. An initial source of errors can be attributed to the data collection. The quality of the estimation of height for each data points depends on the technology applied. Some of the methods available include the ground based or airborne automatic laser scanner which is of a very high resolution and suitable for relatively small areas (Darboux and Huang, 2003). Conventional topographic surveys with a laser theodolite use at the meso scale and with a centimetric accuracy and use of existing contour maps, stereoscopic air-photos or high resolution satellite imagery for the characterization of large areas (Toutin and Cheng, 2002; Poon et al., 2005). The use of DEMS generated from low density altitude data points may result in over estimations of secondary topographic attributes such as the upslope contributing areas (Quinn et al., 1991; Zhang and Montgomery, 1994; Brasington and Richards, 1998) and under estimation of slope gradient (Chaplot et al., 2000; Thompson et al., 2001; Toutin, 2002). Other sources of errors include the spatial structure of altitude and the interpolation technique for DEM generation (Wood and Fisher, 1993; Wilson and Gallant, 2000). The topographic modeler must be particularly careful when selecting the techniques for interpolation between the initial sampling data points of altitude, as this could have a great effect on the quality of DEMS. Many interpolation techniques exist. The question of which is the most appropriate in different contexts is the central question and has stimulated several comparative studies of interpolation accuracy (Weber and Englund, 1992, 1994; Carrara et al., 1997; Robeson, 1997). The existing literature, however, tends to be equivocal as to which interpolation techniques is the most accurate. Some studies (Creutin and Obled, 1982; Laslett and Mc Brantney, 1990; Laslett, 1994; Burrough and Mc Donnell, 1998; Zimmerman et al., 1999; Wilson and Gallant, 2000) indicate that among the many existing interpolation techniques, geostatistical ones better than the others.
In particular, Zimmerman et al. (1999) showed that Kriging yielded better estimations of altitude than IDW did, irrespective of the land form type and sampling pattern. This result is probably due to the ability of Kriging to take into account the spatial structure of data. However, in other studies (Weber and Englund, 1992; Gallichand and Marcotte, 1993; Brus et al., 1996; Declercq, 1996; Aguilar et al., 2005), neighborhood approaches such as IDW or radial basis functions were an accurate as Kriging or even better. Keranc-henko and Bullock (1999) have compared IDW, ordinary Kriging and log normal ordinary Kriging for the soil properties (phosphorous (p) and potassium (k) of 30 experimental fields. They have found that if the underlying data set is log normally distributed and contains less than 200 points, log normal ordinary Kriging generally outperforms both ordinary Kriging and IDW; otherwise ordinary Kriging is more successful. Chaplot et al. (2006) in their study accuracy of interpolation techniques for the derivation of digital elevation models in relation to landform types and data density concluded that under conditions of high C.V, strong spatial structure and strong anisotropy, IDW performs slightly better than the other method. Robinson and Metternich (2006) in their study testing the performance of spatial interpolation techniques for mapping soil properties have used IDW method and concluded that IDW is able to interpolate subsoil PH with a sensible accuracy. Ruhaak (2006) has developed a program which easily interpolates the type of 3D scattered data and produces satisfied results. For the interpolation algorithm has used a modified version of IDW. In this research, preparing the optimized digital elevation model of Jam and Riz basin was studied by use of Inverse Distance Weighting and utilization of GIS technique. With identified cell size of pixels in network with 3 m and determining the rotation angle and measure of axis of standard deviation ellipse, optimized radius was calculated in standard ellipse by use of statistical method. Then optimized power was automatically derived in ArcGIS 9.2 environment. In this method the number of neighbor's points was selected with four repetition points of 3, 5, 7 and 15. However 8 digital elevation models were gained after the mentioned processes. Finally, digital elevation models of 1 to 8 were compared with control points using compare means test in SPSS11.5 software which shown the IDW-3 whit the best conditions recommended as the optimized model.
Jam and Riz basin is located in 25 km toward North Kangan and Jam town and 220 km from Southern part of Boushehr Port. The geographical location of the study area is indicated 51°, 48’, 3.17″E. to 52°, 25’, 14″E and 27°, 44’, 28″N to 28°, 14’, 55″N (Fig. 1).
Jam and Riz basin is surrounded with Zard Kouh range in north and Sarkhan Mountain in north easternen, Haft Chah, Takhteh Siah and Charm Ayne in south eastern, Kachhar in south and Sarcheshme in southern west. The only surface streams of Jam and Hramiaki flow in this area which is by end of spring after conjunction together are formed the main stream of Baghan and finally as the main branch joined to the Mond river. The area of the basin was estimated as 90919.2 ha using Arc GIS 9.2 software. The highest point of the study area shows 1414 m and its lowest point is 57.764 m from the sea level (Modallaldoust, 2007). Several materials have used for generating digital elevation models using IDW interpolation method as follow:
Topographic maps at 1:250000 scale of 1999 from the Iranian Geographical Organization. For the IDW model to producing the elevation points on the maps at 1:25000 scale of 2001 from the National Cartographic Centre of Iran have used. These documents have processed as follow.
First of all they have scanned as topographic maps and then geo referenced in Erdas Imagin 9.1 environment. The border of basin which was already limited on the mentioned maps traced in ArcView3.2a environment and then border vector layer was prepared. In next stage between 15156 elevations points of the base map 10637 points were selected to consider the basin border in the form of digital which was occurred during the process. These points were gained from ground control using Global Positioning System (GPS) during 2003 to 2004 period in the study area. These numbers of elevation points were selected to cover out of the study area. The reason is related to the accurate results from the used model of DEM. Table 1 shows some of the statistics characteristics of these points.
In this method, 2 factors such as neighbor points and point searching radius assumed as model variables. Weight standard distance which is searching radius of standard ellipse (Fig. 2), calculated by the following relations of Eq. 1 and 2 (Ebdon, 1998).
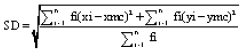 | (1) |
| (2) |
| Table 1: | Descriptive statistics of the elevation points in Jam and Riz basin |
 | |
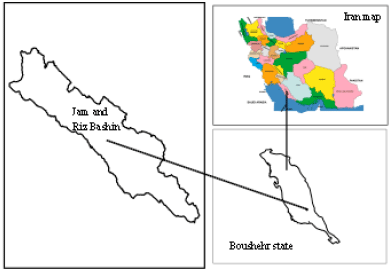 | |
| Fig. 1: | Geographical location of Jam and Riz basin in Iran |
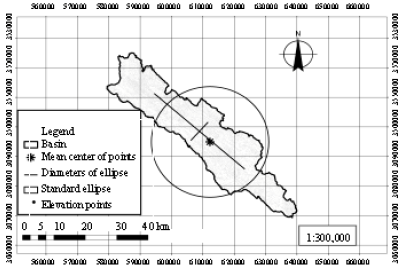 | |
| Fig. 2: | Standard ellipse and standard deviation ellipse for elevation point group |
| xmc and ymc | = | Represent coordinates of average center |
| yi and xi | = | Coordinates of I points |
| fi | = | Abundance of point I and n is the number of points |
During the past three decades, models that solve the catchment and/or solute transport equations in conjunction with an optimization technique have been increasingly used as watershed management tools (Rizzo and Dougherty, 1996; Minsker and Shoemaker, 1998; Zheng and Wang, 2002; Mayer et al., 2001). Simulation-optimization models have been developed for a variety of applications. Standard ellipse is an appropriate way to show the spatial protection of points group (Greene, 1991) but in geographic view the points group may have directional deviation. This problem is very important specially in preparing the numerical models by use of elevation points. In fact, elevation points in different directions to each other can represent several geomorphologic features of special area. The standard deviation ellipse is identified as follows:
| • | Coordinates of average center (xmc, ymc) were calculated on map which is starting points for transmission them. For every points of pi in distribution, coordinates transmission was done as follows: |
| (3) |
After transmission, all points were concentrated on average center.
| • | Rotation angle was calculated using Wong relation (Wong, 2000): |
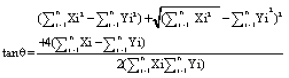 | (4) |
| • | Deviation in length of X and Y axes have derived according to the relations of Eq. 5 and 6 (Levine et al., 1995). |
| (5) |
| (6) |
According to the mentioned methods, the model was tested with 4 categories of 3, 5, 7 and 15 dotted of neighbors points in two radius domains of standard searching circle and standard deviation ellipse. Therefore 8 digital elevation models were extracted then 10637 points equal to 10637 land dots evidence were driven for each model. Finally, the extracted points from each model using SPSS11.5 and by use of means difference test were compared with the land evidence point.
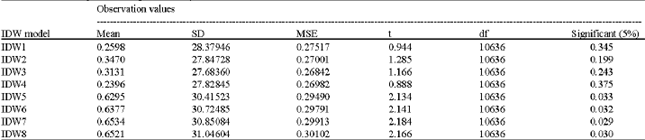
The described expansion of elevation points set based procedure by two hypothesized of spatial dispersion and point's directional deviation was investigated using standard and standard deviation ellipses. The extracted results of this study are presented in Table 2. With an assessment of the necessary factors such as cell size in network (value 3), number of neighbor points (3, 5, 7, 15), standard radius (for standard ellipse) and ellipse rotation angle (in standard deviation ellipse), the optimized power was calculated for each one of 8 digital models. This value is shown in (Table 3). According to this value and the represented factors, digital elevation models was prepared for the study area. With comparing the 10637 extracted points of 8 digital elevation models by SPSS11.5 which due to geographic coordinates is equal to 10637 land evidence points and using of means differences test, the best digital elevation model was obtained. The related results to this analysis are shown in Table 4. In fact, from the gained digital models the accurate one is a model which it’s resulted elevation points has the lowest difference with land elevation points. However it is logical that the data which do not have main differences to land observation in significant 5% is with most accurate. According to the Table 4, four elementary digital models, from IDW1 to IDW4, can not show the main differences with the land observations. To identifying that between 4 digital models which one is with high accuracy, it can be determined with the average of fault value in Table 4. It seems that this data are extremely similar but between them the IDW3 digital elevation model has the lowest mean standard error of 0.26842. Statistical investigation from Table 2 shows individual characteristics of IDW3 which is used seven neighbor points. On the other hand these conclusions show that digital earth data with standard ellipse had sensible response rather than standard deviation ellipse (Fig. 3). The described data have spatial dispersion and the points contain lower directional deviation. However, it can concluded that, IDW3 digital elevation model with optimized power of 3.299 using IDW interpolation is the best digital elevation model for the study area of Jam and Riz basin in Iran which is recommended to used for the same catchments.
Despite of the landscape morphology and land surface of the study area there was a few differences existed between 8 digital elevations models due to the high density sampling which was covered the whole study area. This could have been predictable since increasing the sampling area which is lead to reduce the impact of the interpolation method. The results of this research can be confirmed the similar works of Borgan and Vizzaccara (1997) and Lazzaro and Montefusco (2002). For lower values of sampling density the accuracy of height estimation is related to the choice of neighbor points numbers (Keranc-henko, 2003). IDW method is calculating only some adjacent data points and thus performs well specially for the complex topography when data density increased to a high level (Fisher et al., 1987). The results may help GIS users to select the best alternative for the generation of DEMS. The mentioned technique is recommended not only for its performance on a specific land form type and data density, but also for its capability to a wide range of spatial scales which is applied in this research using two different scales of 1:25000 and 1:250000.
| Table 2: | Characteristics of the test samples in IDW model |
 | |
| Table 3: | The value of optimized power in digital elevation models |
| Table 4: | Test of compare means (paired t- test) for observation elevation value and elevation values of IDW model |
 | |
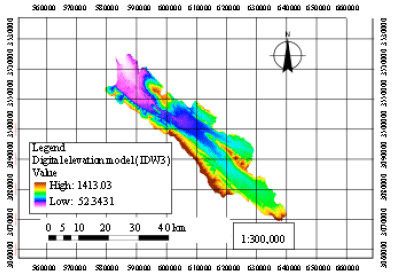 | |
| Fig. 3: | Optimized digital elevation model |
In particular field, DEM quality should be examined through the assessment of primary and secondary DEM derivatives such as slope angle, slope curvature, drainage network and the catchments boundaries as requirement of natural resources to use this technique. These attributes would be more sensitive to the selection of the interpolation technique than the altitude itself. Finally, it can be concluded that the interpolation technique and sampling model of altitude data on the accuracy of watershed management such as hydrologic, soil, land morph modeling needs to be evaluated.
The authors would like to thanks the University of Mazandaran Iran for valuable supports.