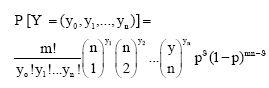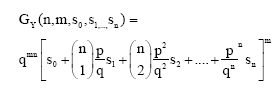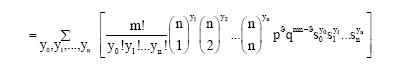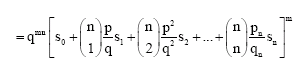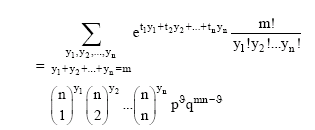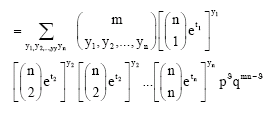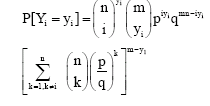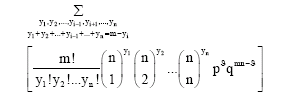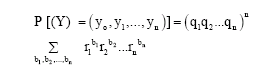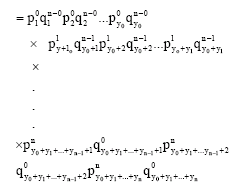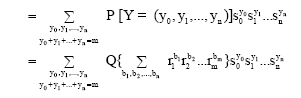Research Article
Probability Distribution of m Binary n-tuples
College of Science, Technology and Applied Arts of Trinidad and Tobago
Shanaz Ansari Wahid
Department of Mathematics and Computer Sciences, The University of the West Indies
Ashok Sahai
Department of Mathematics and Computer Sciences, The University of the West Indies