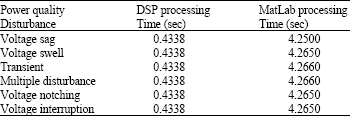
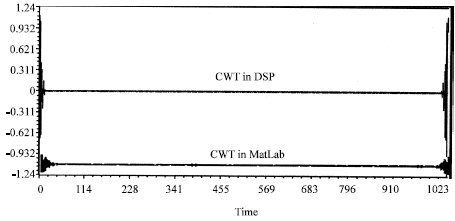
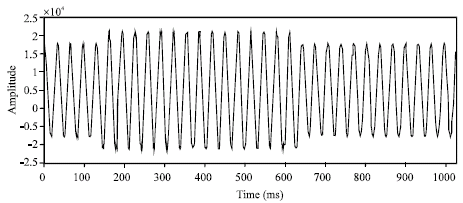
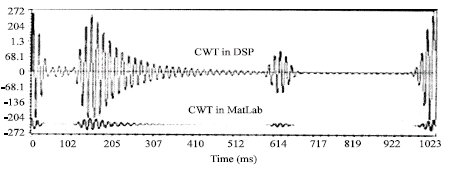
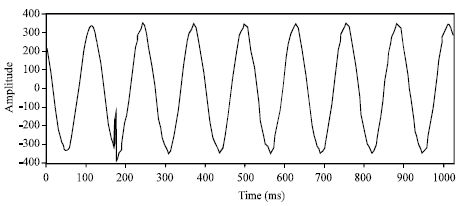
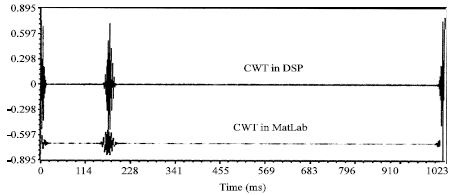
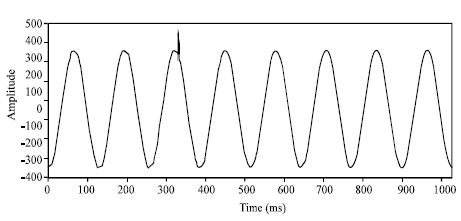
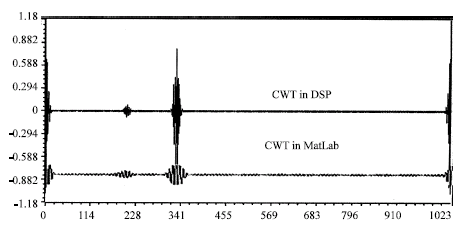
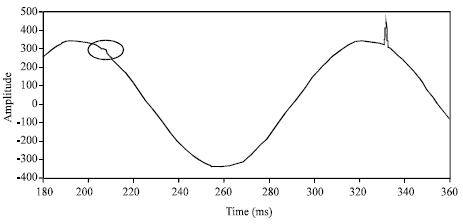
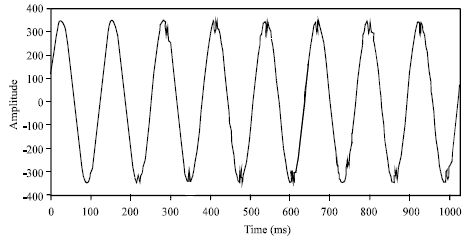
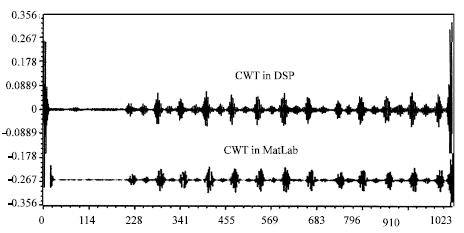
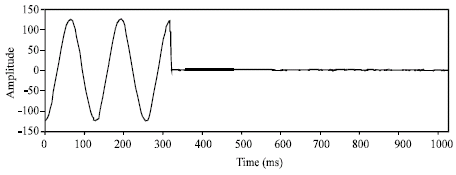
Research Article
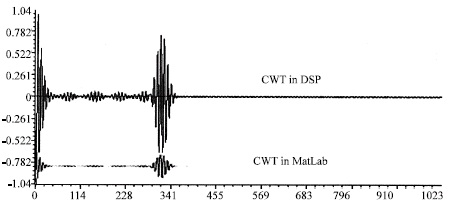
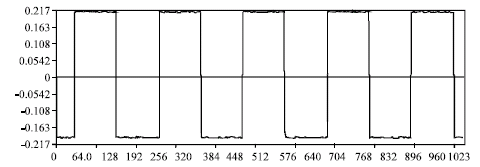
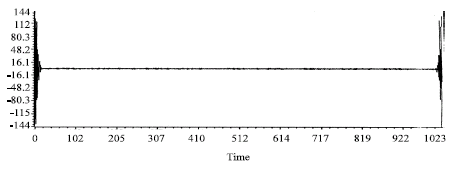
Power Quality Disturbance Detection Using DSP Based Continuous Wavelet Transform
Department of Electrical, Electronic and Systems Engineering, Umversity Rebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia
Azah Mohamed
Department of Electrical, Electronic and Systems Engineering, Umversity Rebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia
Salina Abdul Samad
Department of Electrical, Electronic and Systems Engineering, Umversity Rebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia