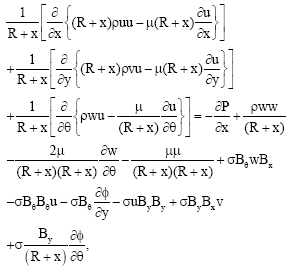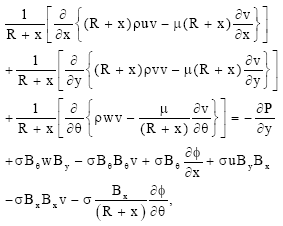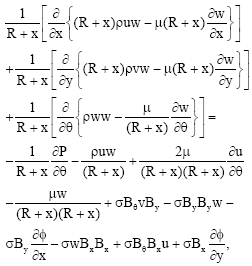Research Article
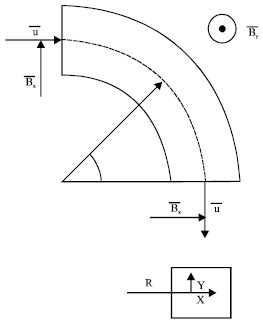
Analyses of MHD Pressure Drop in a Curved Bend for Different Liquid Metals
Pakistan Institute of Engineenng and Applied Sciences, P.O. Nilore, Islamabad, Pakistan
Muhammad Rafique
Department of Physics, University of Azad Jammu and Kashmir Muzaffarabad, 13100 Pakistan
Asad Majid
Pakistan Institute of Engineenng and Applied Sciences, P.O. Nilore, Islamabad, Pakistan
Shahida Jabeen
Department of Physics, University of Azad Jammu and Kashmir Muzaffarabad, 13100 Pakistan