Research Article
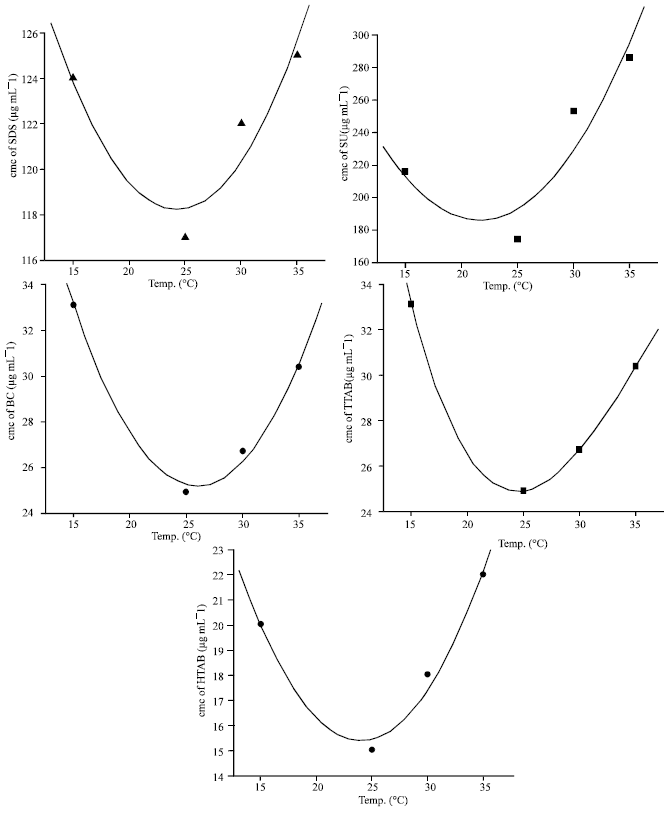
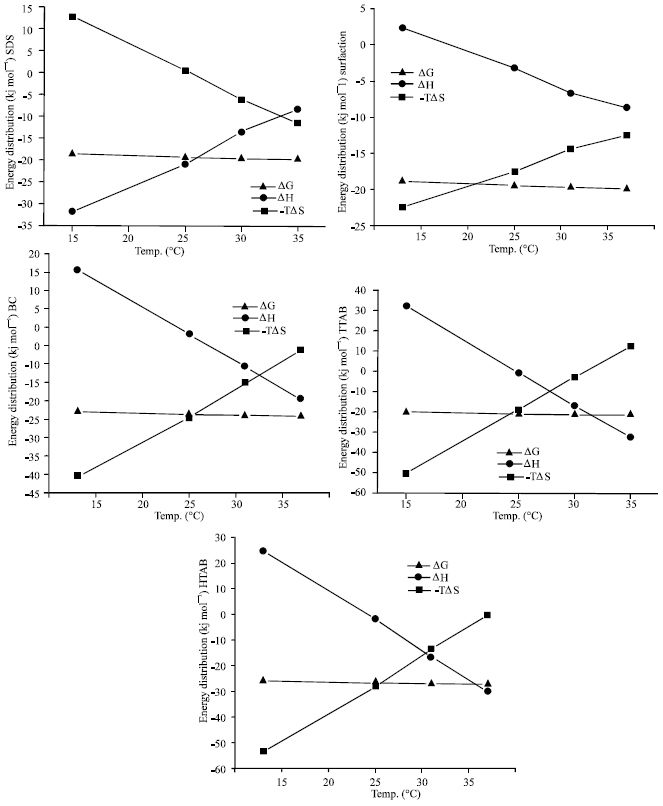
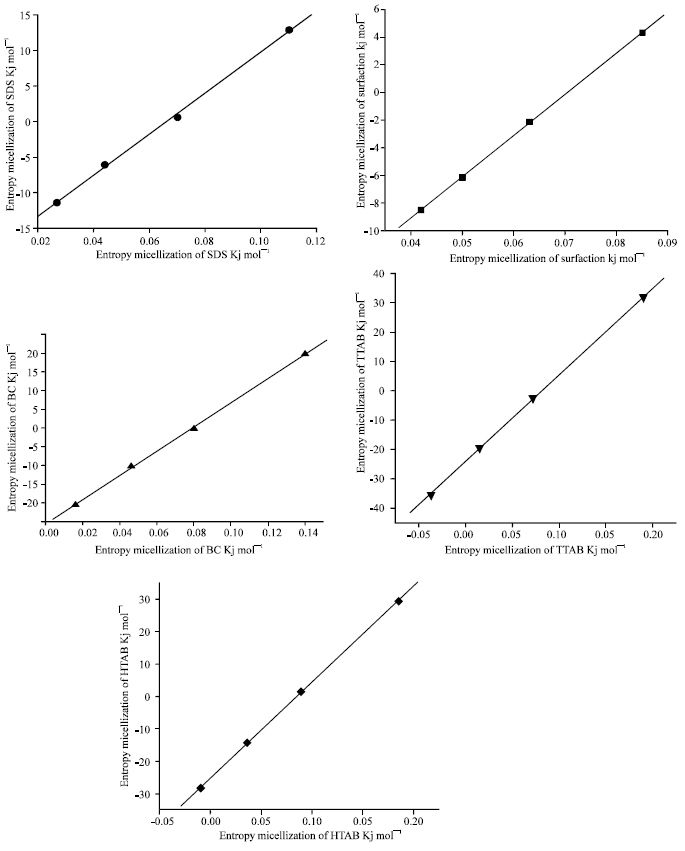
The Effect of Temperature on Thermodynamic Parameters of Micellization of Some Surfactants
Department of Pharmaceutics, School of Pharmacy, Kerman University of Medical Sciences, Kerman, Iran
Mohammadreza Housaindokht
Department of Chemistry, School of Sciences, Ferdowsi University, Mashhad, Iran
Bibi Sedigeh Fazly Bazzaz
Department of Medicinal Chemistry, School of Pharmacy, Mashhad University of Medical Sciences, Mashhad, Iran