Research Article
Simulation of the Electronic Impact Oscillator
Department of Electronic Engineering, Far East University 49 Chung-Hua Road, Tainan 74404, Taiwan
The motion with amplitude constraint of Fig. 1 is consider as mechanical impact oscillator. In the past years, this mass-spring-damping system has been found rich phenomena and given benefit for understanding of impact dynamics (Shaw and Holmes, 1983; Budd et al., 1995; Lee, 2005). Different types of output oscillation, such as periodic and non-periodic (chaotic) motions, can be generated by harmonic excitation. For the purpose of condition monitoring of the system, Lee (2006) calculated the spectrum of Lyapunov exponents for varying the driving frequency. The results showed an agreement with the bifurcation diagram as previous study. In this study, the modeling of the impact oscillator is considered by using electronic circuits. The circuits designed by Azzouz et al. (1984), Zimmerman et al. (1992) and Clark et al. (1995) are modified and presented. The commercial software of MultiSim is used to simulate the circuits and the time series analysis is performed (Multisim User Guide, 2004).
ELECTRONIC CIRCUIT
For a motion constraint of impact oscillator in Fig. 1, the impact dynamics showed a harmonic input oscillation can generate a period or non-period impact motion depends on the control parameter of driving frequency. In this study, the motion constraint of the oscillator is simulated by a feedback diode rectifier circuit as shown in Fig. 2. It consists of a series connection of an ac-voltage source (XFG1), a linear operational amplifier circuit (U3), a nonlinear diode (D1) and two integral circuits (U1 and U2).
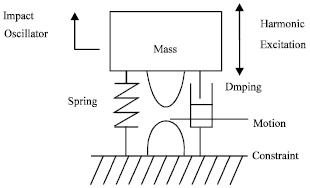 | |
| Fig. 1: | Mechanical impact oscillator |
In this circuit, the impulse impact force is generated by a short period of the positive voltage in the diode circuit D1. In fact, the impact force is proportion to the impact acceleration. Therefore, the velocity and the displacement of impact oscillation can be generated by integral circuits U1 and U2, respectively.
SIMULATION RESULTS
In the following, commercial electronic circuit simulation software, MultiSim, is applied. As the schematic circuit shown in Fig. 2, the electronic impact oscillator circuits are connected by a nonlinear element of diode 1N4001 and three linear elements of operational amplifiers. The input is driven by function generator XFG1 with harmonic sine wave and the output of impact oscillation are illustrated in display XSC1.
For a fixed harmonic input voltage 1.2 V and varying the driving frequency from 50 to 65 Hz, the results shown in Fig. 3 to 5. For 50 Hz input driving frequency, Figure 3a shows an impact-1 oscillation and Fig. 3b shows the phase portrait.
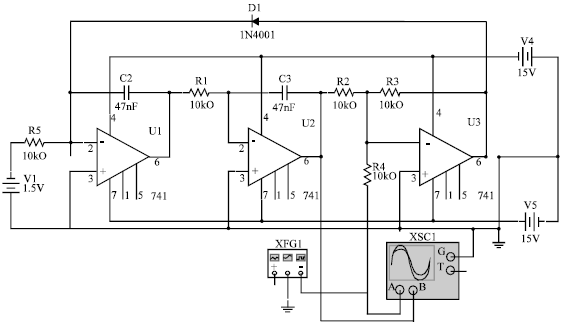 | |
| Fig. 2: | Electronic impact oscillator |
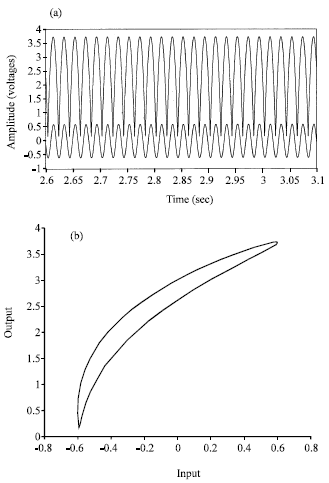 | |
| Fig. 3: | (a) The simulated electronic circuit shows an impact-1 periodic oscillation at driving frequency 50 Hz and amplitude 1.2V (b) Phase portrait of input vs output |
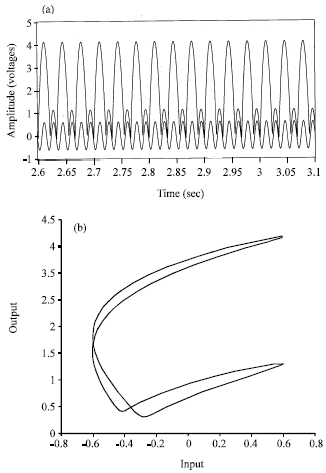 | |
| Fig. 4: | (a) The simulated electronic circuit shows an impact-2 periodic oscillation at driving frequency 60 Hz and amplitude 1.2V (b) Phase portrait of input vs output |
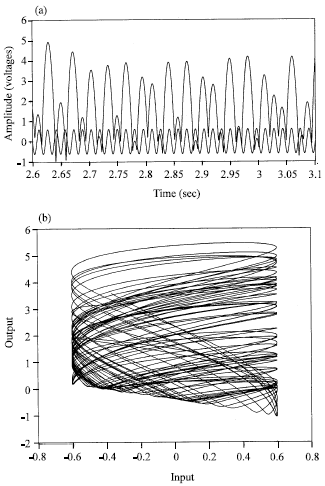 | |
| Fig. 5: | The simulated electronic circuit shows non-periodic impact oscillation at driving frequency 65 Hz and amplitude 1.2V (b) Phase portrait of input vs output |
As the driving frequency increases to 60 Hz, the impact oscillation transits to an impact-2 motion. The bifurcation phenomenon occurs as the results show in Fig. 4. As the driving frequency increases to 65 Hz, the impact oscillator becomes to a non-periodic oscillation. Figure 5a shows a random-like impact motion and Fig. 5b shows a complex phase portrait. These results confirm that a periodic input oscillation can generate a periodic or non-periodic impact oscillation using this circuit. These results are also in agreement with the previous investigation of mechanical impact system.
Through the proposed circuits, a fixed harmonic input voltage can generate a periodic or non-periodic impact oscillation for varying the driving frequency. The phenomena of bifurcation are also observed in this circuit. These results showed the same dynamics occur in mechanical impact oscillator and electronic impact oscillator.
This work was supported by National Science Council (Taiwan), under Grant NSC 9s-2216-M-269-001.