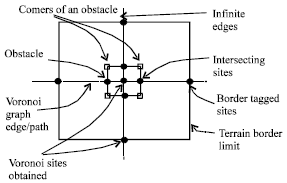
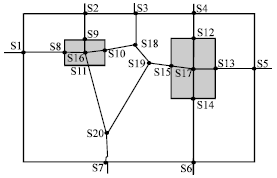
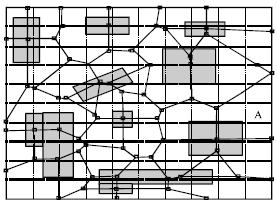
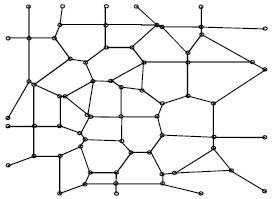
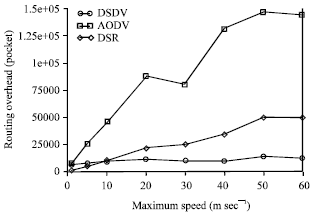
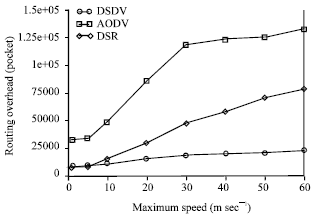
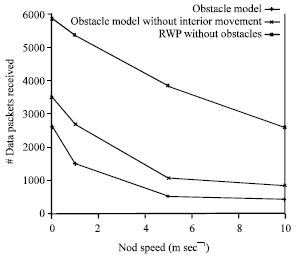
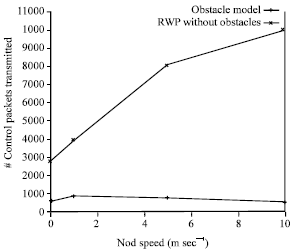
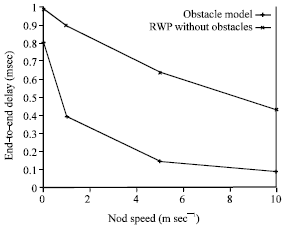
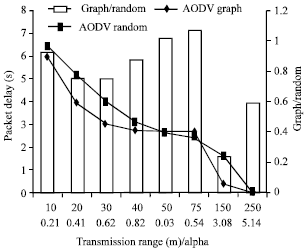
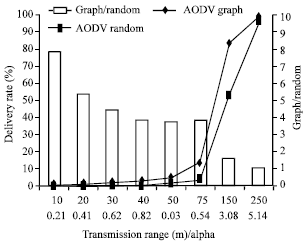
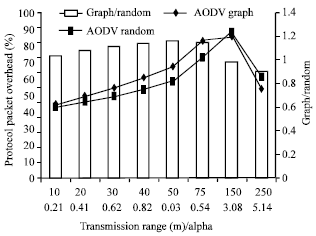
Research Article
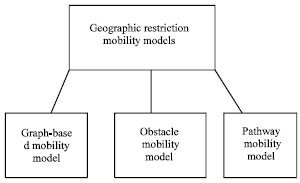
A Survey of Geographic Restriction Mobility Models
Department of Communication and Information Systems, Huazhong University of Science and Technology, Wuhan-430074, Hubei Peoples Republic of China
Wang Furong
Department of Communication and Information Systems, Huazhong University of Science and Technology, Wuhan-430074, Hubei Peoples Republic of China
Yin Wei Hua
Department of Communication and Information Systems, Huazhong University of Science and Technology, Wuhan-430074, Hubei Peoples Republic of China
Sacko .
Department of Communication and Information Systems, Huazhong University of Science and Technology, Wuhan-430074, Hubei Peoples Republic of China